В мире математики существует удивительная задача: как проверить, лежит ли точка на поверхности сферы с заданным уравнением? Этот вопрос настолько глубок и захватывающий, что многие умы столкнулись с ним искали идеальный способ решения.
Однако, несмотря на сложность задачи, математики неистово бросаются к ее решению, применяя логику, аналитику и геометрические преобразования. В поисках клятвенно обещанного алгоритма, они разрабатывают методы и способы, чтобы точно и безошибочно определить, лежит ли точка на поверхности заданной сферы.
Алгоритмы и формулы, воплощенные в программный код или научные доклады, представляют собой настоящий революционный прорыв в области математики и информатики. Поэтому специалисты стараются выбрать оптимальный путь в решении этой задачи, чтобы построить мост между миром абстрактных чисел и реальности, где нам нужно знать точное положение каждой точки на поверхности сферы.
Методы проверки принадлежности точки к геометрическому объекту

В данном разделе рассматриваются различные методы, позволяющие проверить, принадлежит ли точка заданной сфере. Вместо использования прямых определений, мы сосредоточимся на анализе свойств и особенностей геометрического объекта в контексте точки.
Один из методов, который можно использовать для проверки принадлежности точки к сфере, основывается на вычислении расстояния между центром сферы и данной точкой. Если это расстояние равно радиусу сферы, то точка лежит на поверхности сферы.
Другой метод принимает во внимание положение точки в трехмерном пространстве. Точка считается лежащей на сфере, если расстояние от нее до центра сферы в сочетании с ее координатами удовлетворяет уравнению сферы.
- Метод пересечения сферы и прямой позволяет определить, принадлежит ли точка сфере или находится вне ее. Если прямая, проходящая через центр сферы и данную точку, пересекает поверхность сферы, то точка лежит на сфере.
- Еще одним методом проверки принадлежности точки к сфере является анализ ее координат в системе радиус-векторов. Путем вычисления нормы радиус-вектора точки и сравнения ее со значением радиуса сферы можно установить, находится точка на сфере или вне ее.
- Также существуют алгоритмы, основанные на применении тригонометрии и геометрических свойств сферы для проверки принадлежности точки.
Точки, принадлежащие сфере, обладают специфическими свойствами и подчиняются определенным условиям. Использование различных методов и алгоритмов позволяет эффективно проверять принадлежность точки к сфере и определять ее положение на поверхности данного геометрического объекта.
Использование геометрического описания сферы для проверки положения точки
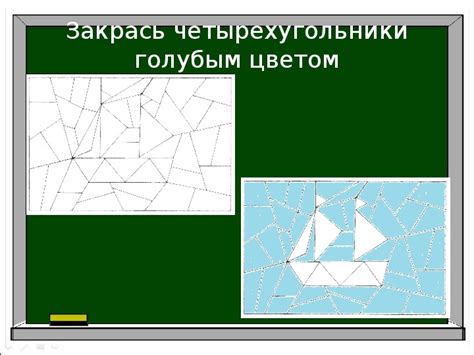
В данном разделе рассмотрим применение геометрического описания сферы для определения, находится ли данная точка в заданном положении.
Для этого используется уравнение сферы, которое позволяет задать геометрическую форму сферы с ее центром и радиусом. Воспользовавшись этим уравнением, можно проверить, находится ли конкретная точка на поверхности сферы.
Для определения положения точки достаточно подставить координаты этой точки в уравнение сферы и рассчитать значение выражения. Если значение равно нулю, то точка лежит на поверхности сферы, а если значение отлично от нуля, то точка находится вне сферы или в ее внутреннем пространстве.
Использование уравнения сферы для проверки положения точки является важным инструментом в различных областях, таких как геометрия, компьютерная графика или науки о материалах. С его помощью можно быстро и эффективно определять положение точки относительно заданной сферы.
Для более глубокого понимания и применения данного метода, полезно ознакомиться с примерами, в которых иллюстрируется использование уравнения сферы для проверки положения точки на поверхности или внутри сферы.
Таким образом, использование уравнения сферы является эффективным способом для проверки положения точки и может быть полезным во множестве практических ситуаций, связанных с геометрией пространства.
Использование векторных вычислений для проверки точки на принадлежность к сфере
В данном разделе рассматривается метод, основанный на векторных вычислениях, для проверки, лежит ли точка на поверхности сферы. Вместо традиционного подхода с использованием уравнения сферы, мы сфокусируемся на векторных операциях, которые позволяют эффективно определить принадлежность точки к сфере.
Использование векторных вычислений предоставляет удобный способ решения этой задачи. Мы можем представить сферу в виде набора точек в трехмерном пространстве и использовать векторы для определения положения точки относительно сферы. Для этого необходимо взять вектор, направленный от центра сферы к проверяемой точке, и проверить, пересекает ли он поверхность сферы.
Этот подход позволяет упростить алгоритм проверки и реализовать его более эффективно с помощью векторных операций. Достоинством этого метода является его простота и универсальность, что позволяет применять его для проверки точек на принадлежность к сфере с любым уравнением.
| Преимущества | Недостатки |
|---|---|
| Простота реализации | Требуется вычисление векторов |
| Универсальность | Может быть несколько сложнее в понимании для начинающих |
| Эффективность | - |
Таким образом, использование векторных вычислений предоставляет эффективный и универсальный метод для проверки точек на принадлежность к сфере. Рассмотренный подход основан на векторных операциях и позволяет более просто и эффективно решать данную задачу, внося разнообразие в способы проверки точек на принадлежность сфере.
Установление местоположения точки относительно геометрической фигуры
В данном разделе мы рассмотрим методы и алгоритмы, позволяющие определить положение точки относительно сферической поверхности. Эта задача возникает во многих областях, от геометрии до компьютерной графики, и имеет свои уникальные подходы для решения.
Основной идеей является проверка, находится ли точка внутри сферы, на границе или за ее пределами. Для этого необходимо использовать математические модели и уравнения, которые описывают данную сферу. Решение этой задачи может быть как аналитическим, основанным на точных вычислениях, так и численным, когда требуется приближенное определение.
Для аналитического решения задачи определения положения точки на сфере используются такие методы, как проверка уравнения сферы на выполнение или невыполнение, а также использование неравенств для определения взаимного расположения координат точки и параметров сферы. Дополнительно, при решении этой задачи может понадобиться использование геометрических преобразований и алгебраических выкладок.
Но наиболее эффективным методом является численное решение, которое базируется на аппроксимации и приближенных вычислениях. Используя итеративные алгоритмы и вычислительные методы, можно найти приближенное положение точки относительно заданной сферы с высокой степенью точности. Такой подход особенно полезен в случаях, когда точное решение невозможно или требует значительных вычислительных ресурсов.
Об использовании уравнения сферы для анализа геометрической задачи

В данном разделе мы рассмотрим важный метод решения геометрических задач, основанный на использовании уравнения сферы. Этот подход позволяет нам определить, принадлежит ли точка заданной сфере, и применяется в различных областях, включая геодезию, компьютерную графику и физику.
Основной принцип метода
Идея заключается в использовании уравнения сферы для описания этой геометрической фигуры. Уравнение сферы определяет все точки, находящиеся на равном удалении от центра сферы. Если дана точка, для определения ее положения относительно сферы мы можем подставить ее координаты в уравнение сферы и проверить, выполняется ли оно. Если уравнение выполняется, то точка лежит на сфере, иначе она находится вне сферы.
Нюансы применения и вариации метода
Важно отметить, что в реальных задачах мы можем сталкиваться с различными вариациями уравнения сферы, включая задание в параметрической или канонической форме. При этом необходимо адаптировать наш метод проверки точки под конкретную форму уравнения.
Практическое применение метода
Использование уравнения сферы для решения задач является широко распространенным и позволяет нам эффективно определять принадлежность точки сфере в трехмерном пространстве. Этот метод находит применение в различных науках и инженерных приложениях, в том числе в моделировании телекоммуникационных сетей, анализе региональных данных и задачах определения границы объектов.
Метод перебора: эффективный способ определения положения точки на заданной сфере

В этом разделе мы рассмотрим один из методов решения задачи определения положения точки на сфере с помощью перебора. Этот метод основан на систематическом итеративном процессе, который позволяет найти ответ, проверяя различные варианты расположения точки на заданной сфере.
Основной принцип метода перебора заключается в исследовании множества возможных вариантов положения точки на сфере с использованием заданных уравнений. В ходе итераций метод последовательно проверяет каждый из возможных вариантов и сравнивает результаты с требуемыми условиями. Таким образом, метод перебора позволяет эффективно определить, лежит ли данная точка на заданной сфере.
Используя этот метод, можно достичь точного результата, основываясь на заданных уравнениях, которые описывают геометрические особенности сферы. Перебор всех возможных вариантов положения точки позволяет исключить ошибки и исследовать все возможные ситуации, что делает метод перебора надежным и точным инструментом для решения задачи определения положения точки на сфере.
Преимущества использования метода перебора состоят в его простоте и достоверности результатов. Этот метод позволяет решить задачу без необходимости проведения сложных математических вычислений или применения специализированного программного обеспечения. Благодаря простоте и понятности алгоритма, метод перебора может быть легко реализован на различных языках программирования.
Вопрос-ответ

Как проверить, лежит ли точка на сфере с заданным уравнением?
Для проверки того, лежит ли точка на сфере с заданным уравнением, необходимо подставить координаты точки в уравнение сферы и проверить, выполняется ли равенство. Если равенство выполняется, то точка лежит на сфере, иначе - точка не лежит на сфере.
Что означает то, что точка лежит на сфере?
Когда говорят, что точка лежит на сфере, это означает, что эта точка находится на поверхности сферы, соответствующей заданному уравнению. То есть, если подставить координаты этой точки в уравнение сферы, то равенство будет выполняться.
Как проверить, лежит ли точка внутри сферы?
Для проверки, лежит ли точка внутри сферы с заданным уравнением, нужно подставить ее координаты в уравнение сферы и проверить, выполняется ли неравенство: (x - a)² + (y - b)² + (z - c)²Как определить, лежит ли точка за пределами сферы?
Чтобы определить, лежит ли точка за пределами сферы с заданным уравнением, необходимо подставить координаты точки в уравнение сферы и проверить, выполняется ли неравенство: (x - a)² + (y - b)² + (z - c)² > r². Если неравенство выполняется, то точка лежит за пределами сферы, если неравенство не выполняется или выполняется равенство, то точка не лежит за пределами сферы.Как проверить, лежит ли точка на сфере с заданным уравнением?
Для проверки того, лежит ли точка на сфере с заданным уравнением, необходимо подставить значения координат этой точки в уравнение сферы. Если полученное равенство выполняется, то точка лежит на сфере, в противном случае - нет.



