В мире математики существуют законы и закономерности, которые кажутся непостижимыми для нас, простых смертных. Одним из таких загадочных объектов является прямоугольный треугольник. Известно, что он обладает свойствами, которые остаются скрытыми от нас до тех пор, пока мы сами не начнем исследовать их. Что же скрывается за таинственными терминами "катет" и "гипотенуза"? Какие их особенности и какие формулы лежат в основе этих связей?
Задача для нас - коснуться загадочного происхождения и глубинных свойств этих фигур. Катеты, эти два строения, сходящиеся в угле, наводят на размышления о некой внутренней связи. Кажется, что они не просто сосуществуют в прямоугольном треугольнике, а силой своей уравновешивают друг друга в данный момент времени. Они сочетаются вокруг гипотенузы, образуя нечто большее, чем просто геометрическую фигуру. Давайте же углубимся в анализ этой гармонии и разгадаем все их секреты!
Важность понимания и использования свойств прямоугольного треугольника не может быть переоценена. Ведь именно благодаря этим связям и формулам мы можем решать разнообразные задачи и применять их в реальной жизни. От строительства до астрономии, прямоугольные треугольники переплетены с нашими судьбами и заветными целями. Именно поэтому мы должны разобраться в них, раскрыть все их возможности и научиться использовать их в своей повседневной деятельности. Откроем для себя новые грани этой увлекательной геометрической тайны и освоим некоторые удивительные концепции, связанные с этими фигурами!
Основные характеристики и свойства геометрической фигуры
Столкнувшись с треугольником, каждый из нас немедленно узнает его по форме и размеру. Каждый треугольник имеет свои уникальные характеристики, которые определяют его свойства и геометрическую структуру.
Прямоугольный треугольник - это треугольник, внутри которого есть прямой угол, то есть угол в диапазоне от 90 до 180 градусов. Такой угол может быть определен двумя сторонами, называемыми катетами, и гипотенузой, которая является наибольшей стороной треугольника. Часто прямоугольный треугольник используется в геометрии для решения задач и вычислений в различных областях, начиная от архитектуры и инженерии до физики и геодезии.
Одно из важных свойств прямоугольного треугольника - теорема Пифагора, которая гласит, что квадрат гипотенузы равен сумме квадратов катетов. Эта формула стала одной из основ физических и математических вычислений и нашла широкое применение в различных областях науки и технологий. Эта теорема позволяет нам вычислять длину прямоугольного треугольника, если известны длины других двух сторон.
Не только длины сторон имеют значение в прямоугольном треугольнике. Он также имеет свои уникальные углы и отношения сторон, которые помогают нам понять его форму и свойства. Углы прямоугольного треугольника можно классифицировать как прямой угол, а также острые углы, которые составляются из сторон, противоположных друг другу относительно гипотенузы. Отношение между сторонами треугольника может быть выражено с помощью тригонометрических функций, таких как синус, косинус и тангенс.
- Прямоугольный треугольник - это треугольник, содержащий прямой угол.
- Гипотенуза - наибольшая сторона треугольника, находяющаяся напротив прямого угла.
- Катеты - две меньшие стороны треугольника, примыкающие к прямому углу.
- Теорема Пифагора - квадрат гипотенузы равен сумме квадратов катетов: a^2 + b^2 = c^2.
- Углы прямоугольного треугольника - прямой угол и два острых угла.
- Отношение между сторонами треугольника может быть выражено с помощью тригонометрических функций.
Взаимосвязь между длиной сторон прямоугольного треугольника
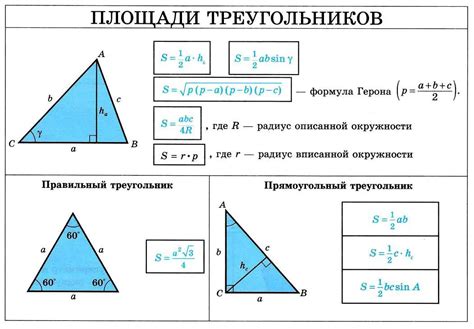
При изучении прямоугольного треугольника часто важно понять, как связаны между собой длины его сторон. Особое внимание уделяется соотношению между катетами и гипотенузой, которое позволяет решать различные задачи и находить недостающие значения.
Это взаимосвязь можно выразить с помощью нескольких основных формул, которые позволяют найти длину катета или гипотенузы, исходя из известных значений. Например, одной из таких формул является теорема Пифагора, которая устанавливает, что квадрат длины гипотенузы равен сумме квадратов длин катетов.
- Степень сжатия: соотношение катетов и гипотенузы напрямую влияет на степень сжатия треугольника.
- Отношение двух сторон: длина катета может быть как больше, так и меньше длины гипотенузы. Отношение между ними может быть описано с помощью различных коэффициентов.
- Аналитическое решение: с использованием формул и известных значений можно решать различные задачи, например, находить площадь треугольника.
- Зависимость от углов: соотношение катетов и гипотенузы также зависит от значений углов в прямоугольном треугольнике. Изменение углов может привести к изменению этого соотношения.
Понимание соотношения между катетами и гипотенузой прямоугольного треугольника является основой для решения задач по геометрии и физике. При нахождении неизвестных значений сторон треугольника необходимо учитывать, как эти стороны связаны между собой, чтобы получить корректный и точный результат.
Теорема Пифагора и ее применение к геометрии прямоугольных треугольников
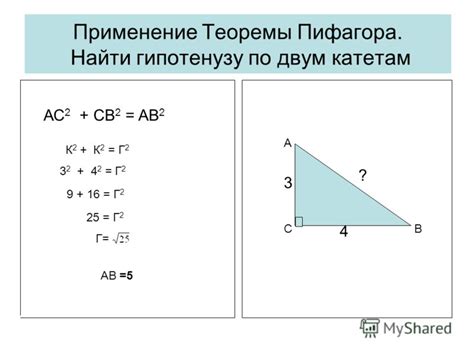
В геометрии есть одно из самых удивительных открытий, которое позволяет нам раскрыть скрытые связи между сторонами прямоугольных треугольников и использовать их для решения различных задач. Это так называемая Теорема Пифагора.
Теорема Пифагора, названная в честь великого древнегреческого математика, гласит, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Это весьма простое и краткое утверждение, но его применение в геометрии огромно. Благодаря Теореме Пифагора мы можем находить длину одной из сторон прямоугольного треугольника, если известны длины двух других сторон. Также, используя эту теорему, мы можем проверять, является ли треугольник прямоугольным, искать отношения между его сторонами и применять их для решения различных задач.
Теорема Пифагора имеет широкое применение в реальной жизни. Например, она используется в строительстве и архитектуре для нахождения длин сторон прямоугольных участков, а также в навигации для определения расстояний между точками на карте. Это позволяет нам точно расчитывать и измерять расстояния без необходимости их физического измерения.
Исторический контекст открытия Теоремы Пифагора в то или иное время интересовал многих математиков. Это учение является основой геометрии и имеет непосредственное отношение к прямоугольным треугольникам. Его полезность в тех случаях, когда требуется найти длину стороны прямоугольного треугольника, делает его неотъемлемой частью образования в области геометрии.
Методы вычисления длины сторон прямоугольного треугольника

В математике существует несколько способов определения длины катета и гипотенузы прямоугольного треугольника, которые позволяют решать задачи, связанные с геометрией и тригонометрией. Зная эти методы, можно с легкостью определить искомые значения и использовать их в дальнейших вычислениях.
Один из методов подсчета длины катета основан на использовании теоремы Пифагора. Эта формула устанавливает связь между длиной гипотенузы и длинами катетов прямоугольного треугольника. Путем подстановки известных значений, можно найти длину катета.
Другим методом вычисления длины катета при известной гипотенузе является применение тригонометрических функций. Например, с помощью функции синуса можно определить длину катета, зная угол между гипотенузой и катетом, а также длину гипотенузы.
Для нахождения длины гипотенузы прямоугольного треугольника также можно воспользоваться теоремой Пифагора. В данном случае известными значениями являются длины обоих катетов, и подстановка их в формулу позволит вычислить искомую величину.
Решение задач: приложение свойств прямоугольного треугольника
В этом разделе мы рассмотрим практические примеры решения задач, в которых применяются основные свойства и формулы, характерные для прямоугольных треугольников. Решение таких задач позволяет нам применить полученные знания и раскрыть их практическую значимость.
Пример 1. Определение длины гипотенузы
Предположим, что у нас имеется прямоугольный треугольник с известными значениями длины одного катета и гипотенузы. Задача состоит в определении длины второго катета. Для решения данной задачи мы можем воспользоваться одним из основных свойств прямоугольных треугольников - теоремой Пифагора.
Решение:
Исходя из теоремы Пифагора, согласно которой квадрат длины гипотенузы равен сумме квадратов длин катетов, мы можем записать уравнение:
а² + b² = c²,
где a и b - длины катетов, а c - длина гипотенузы. Зная значения двух известных сторон, мы можем выразить неизвестную длину катета:
а² = c² - b²,
а = √(c² - b²).
Таким образом, мы можем определить длину второго катета, зная значения длины гипотенузы и одного из катетов.
Пример 2. Расчет площади прямоугольного треугольника
Предположим, что у нас имеется прямоугольный треугольник, и нам необходимо вычислить его площадь. Для решения данной задачи мы можем воспользоваться формулой для расчета площади треугольника: S = (a * b) / 2, где a и b - длины катетов.
Решение:
Исходя из данной формулы, мы можем записать:
S = (a * b) / 2.
Подставляя известные значения длин катетов, мы можем вычислить площадь треугольника.
Это всего лишь два примера использования основных свойств и формул прямоугольных треугольников. Здесь мы видим, как эти знания могут быть применены на практике для решения разнообразных задач. Знание основных свойств и формул прямоугольных треугольников является важным инструментом в геометрии и может использоваться в различных сферах обучения и работы.
Вопрос-ответ

Как найти длину катета прямоугольного треугольника, если известна длина гипотенузы?
Длину катета прямоугольного треугольника можно найти по теореме Пифагора. Если известна длина гипотенузы (пусть она равна с), а один из катетов имеет длину х, то второй катет можно найти по формуле: катет = √(c^2 - x^2).
Как найти длину гипотенузы прямоугольного треугольника, если известны длины обоих катетов?
Длину гипотенузы прямоугольного треугольника можно найти также по теореме Пифагора. Если известны длины обоих катетов (пусть первый катет равен а, а второй - b), то гипотенуза будет равна √(a^2 + b^2).
Как использовать свойства прямоугольного треугольника для решения геометрических задач?
Свойства прямоугольного треугольника очень полезны при решении геометрических задач. Например, зная длины катетов или гипотенузы, вы можете находить длину других сторон треугольника, вычислять площадь треугольника или находить углы. Они также могут помочь в нахождении высоты, радиуса вписанной окружности и других величин. Поэтому, знание свойств прямоугольного треугольника может быть очень полезным при решении различных геометрических задач.
Какой угол в прямоугольном треугольнике является прямым?
В прямоугольном треугольнике один из углов равен 90 градусам, то есть является прямым углом. Такой угол образуется между гипотенузой и одним из катетов.
Как проверить, является ли треугольник прямоугольным?
Существует несколько способов проверки прямоугольности треугольника. Например, можно использовать теорему Пифагора: если квадрат длины гипотенузы равен сумме квадратов длин двух катетов, то треугольник является прямоугольным. Также можно найти все углы треугольника и проверить, есть ли среди них прямой угол. Если хотя бы один из углов равен 90 градусам, то треугольник прямоугольный.
Как определить длину катета прямоугольного треугольника, если известна длина гипотенузы?
Для определения длины катета прямоугольного треугольника по известной длине гипотенузы можно использовать теорему Пифагора. По этой теореме, квадрат длины гипотенузы равен сумме квадратов длин катетов. Следовательно, чтобы найти длину одного из катетов, нужно извлечь корень квадратный из разности квадрата длины гипотенузы и квадрата длины другого катета.