Великая математика кроется в каждом уголке нашего мира. Мысль о числах, формах и расчетах поражает своей универсальностью и проникает в самые глубины нашего сознания. Каждая задача, будь то нахождение неизвестного или поиск зависимостей, предлагает нам погрузиться в мир смыслов и символикой чисел. Сегодня мы отправимся в захватывающее путешествие по пространству геометрических фигур и узнаем, как найти длину стороны определенной фигуры, известной своей площадью.
Надеждой нашим дороговым спутником будет квадрат – идеально симметричная фигура, которая не перестает восхищать своей простотой и элегантностью. Ничто не приближало сердца ученых так близко к математической гармонии, как этот образ с четырьмя равными сторонами и прямыми углами. Квадрат – символ сущности геометрии, отражающий основные законы и формы, из которых состоит наш мир.
В самом начале нашей поисковой экспедиции нас ожидает самый простой и одновременно тревожный вопрос – как найти длину стороны квадрата? Казалось бы, что может быть проще: все стороны равны! Однако, есть ситуации, когда одна из сторон неизвестна, и нам нужно заполнить этот пробел в пространстве. Важно знать, что каждая сторона квадрата – это целое число и она всегда положительна, так как отрицательного значения длины стороны не существует в реальности.
Площадь квадрата и способы ее вычисления
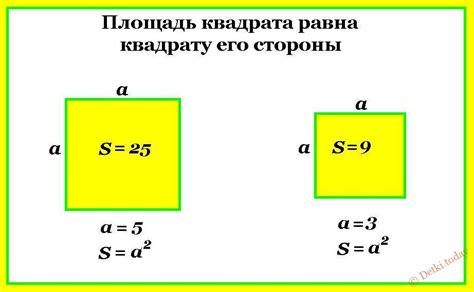
Одним из доступных методов вычисления площади квадрата является использование его стороны. Квадрат – это фигура с четырьмя равными сторонами, поэтому найдя длину одной стороны, можно легко вычислить площадь. Конкретный пример такой задачи может быть следующим: дана площадь квадрата, равная 144 см². Теперь мы хотим найти длину его стороны, используя доступные методы подсчета.
- Используя синтетический подход, можно поделить площадь на количество сторон квадрата и извлекать длину каждой стороны с помощью подходящих строительных или измерительных инструментов.
- Альтернативный метод включает использование геометрической формулы, основанной на знании площадей и связей между различными геометрическими фигурами. Например, можно вычислить площадь прямоугольника, зная его длину и ширину, и затем определить сторону квадрата, зная, что все его стороны равны друг другу.
- Другой подход может основываться на использовании графических средств, таких как графики или диаграммы. Построив квадрат и разделив его на более мелкие фигуры, мы можем сосредоточиться на вычислении площадей этих более простых форм, что позволит нам определить сторону квадрата.
Итак, площадь квадрата важна для определения его размеров и функций. Для вычисления стороны квадрата можно использовать несколько доступных методов, которые опираются на геометрические, синтетические или графические подходы. Изучив эти методы, вы сможете решить задачи, связанные с нахождением стороны квадрата по известной площади без использования формул и специальных инструментов.
Какие формулы позволяют определить размер каждой стороны квадрата, исходя из его площади?
В математике, когда имеется квадрат, нам часто требуется определить длину его стороны. Также, нам могут быть даны площадь и различные параметры, и мы должны найти значения сторон квадрата. Возможны несколько способов осуществления таких расчетов. Зная формулы, мы можем найти сторону квадрата при его заданной площади, и этот процесс требует применения определенных математических операций.
Базовые понятия математики: основа для решения задач

В мире чисел, формул и уравнений существуют основные понятия, которые служат фундаментом для решения различных математических задач. Понимание этих базовых концепций позволяет нам ориентироваться в математическом пространстве и находить решения наших задач.
Одно из таких понятий - площадь. Площадь - это мера поверхности, покрытой фигурой, и обозначает количество единиц площади, которые можно разместить внутри данной фигуры. В нашем случае мы будем обсуждать площадь квадрата. Квадрат - это фигура с четырьмя равными сторонами и углами, известными как прямые углы.
Когда мы имеем задачу о нахождении стороны квадрата по его площади, нам необходимо применить знания и формулы, связанные с понятиями площади и квадрата. В данном случае, мы знаем, что площадь квадрата равна 144 квадратным сантиметрам. Для решения этой задачи мы можем применить обратную операцию взятия квадратного корня, чтобы найти длину стороны квадрата. Это позволит нам восстановить размеры исходной фигуры и найти решение задачи.
Детальный разбор основной формулы вычисления размера стороны квадрата исходя из его площади
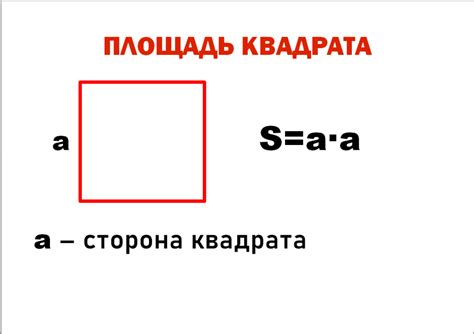
В данном разделе будет представлен подробный анализ формулы, позволяющей определить сторону квадрата на основе известной площади без явного указания численных значений. Мы рассмотрим каждый компонент этой формулы и объясним его предназначение, давая вам полное понимание процесса вычисления.
| Символ | Обозначение | Описание |
|---|---|---|
| A | Площадь квадрата | Известное значение площади квадрата, которое мы используем в формуле |
| s | Сторона квадрата | Неизвестная величина, которую мы пытаемся определить |
В основе формулы лежит понятие площади квадрата, которое определяется как произведение длины одной из его сторон на саму себя. Итак, мы знаем, что площадь квадрата (A) равна s^2, где s - сторона квадрата.
Для вычисления стороны квадрата (s) по известной площади необходимо воспользоваться обратной операцией к возведению в квадрат, а именно - извлечением квадратного корня. Таким образом, исходная формула для определения стороны квадрата будет иметь следующий вид:
s = √A
Разложим формулу на составляющие:
1. A - известная площадь квадрата, которую мы получаем от пользователя или из другого источника данных.
2. √ - символ квадратного корня, с помощью которого мы извлекаем корень из площади квадрата. Операция корневого извлечения позволяет нам найти значение стороны квадрата в отсутствие конкретных численных данных.
3. s - найденная сторона квадрата, которую мы определяем, используя известную площадь и операцию корневого извлечения.
Итак, при помощи данной формулы вы сможете определить размер стороны квадрата на основе его площади без необходимости знать конкретные численные значения. Теперь вы знакомы с каждым элементом этой формулы и понимаете, как они взаимосвязаны и влияют на итоговый результат.
Вопрос-ответ

Как найти сторону квадрата по его площади 144 см2?
Чтобы найти сторону квадрата по его площади, необходимо взять квадратный корень из площади. В данном случае, площадь равна 144 см2, поэтому достаточно извлечь квадратный корень из 144. Так как корень из 144 равен 12, сторона квадрата составляет 12 см.
Какую формулу использовать для нахождения стороны квадрата по заданной площади?
Для нахождения стороны квадрата по его площади можно использовать формулу S = a^2, где S - площадь квадрата, а - сторона квадрата. Таким образом, если известна площадь S, то можно найти сторону квадрата a, вычислив квадратный корень из S.
Как найти площадь квадрата, если известна его сторона?
Если известна сторона квадрата, то площадь можно найти, возведя эту сторону в квадрат. То есть, чтобы найти площадь квадрата, достаточно умножить его сторону на саму себя. Например, если сторона квадрата равна 12 см, то его площадь будет равна 144 см2.
Можно ли найти сторону квадрата, если известна только его диагональ?
Нет, нельзя найти сторону квадрата, зная только его диагональ. Диагональ квадрата связана со стороной по теореме Пифагора, но для нахождения стороны требуется знать еще одну измеряемую величину, например, площадь, периметр или диаметр окружности, вписанной в этот квадрат.
Как проверить правильность найденной стороны квадрата?
Для проверки правильности найденной стороны квадрата можно воспользоваться формулой для вычисления площади. Если сторона квадрата равна а, то его площадь будет равна а^2. Сравните полученное значение площади с изначально заданной площадью. Если они совпадают, значит найденная сторона верна.
Как найти сторону квадрата по его площади 144 см2?
Чтобы найти сторону квадрата по его площади, необходимо извлечь квадратный корень из площади. В данном случае, чтобы найти сторону квадрата с площадью 144 см2, нужно извлечь квадратный корень из 144, что равно 12. Таким образом, сторона квадрата равна 12 см.