Размышления о геометрии всегда побуждают нас обнаружить едва заметные детали, раскрыть великолепие, скрытое в простейших формах. Геометрические фигуры - это мусынка рациональных отношений в природе, где законы, стремящиеся к совершенству, создают великолепные образы. Величественная окружность, симметрично расположенная в пространстве, привлекает внимание и вызывает интерес к своим особенностям.
Один из самых увлекательных моментов, связанных с окружностью, заключается в определении местоположения точек на ее поверхности. В самом простом случае мы можем представить себе танцора, который грациозно перемещается по круговой дорожке вокруг центра окружности. Однако, что происходит, когда мы хотим обнаружить, где будет находиться этот танцор через определенное время или после определенного угла поворота? Это вопрос, вызывающий умственное беспокойство и провоцирующий нашу фантазию.
При погружении в завораживающий мир геометрии окружности мы открываем новые способы расчета и определения положения точек, а также понимаем гармоничные законы, регулирующие их движение. Здесь мы познакомимся с фундаментальными концепциями нахождения точек на окружности, исследуем их особенности и попытаемся обнаружить идеальные сочетания, лежащие в основе их расположения на окружности.
Природные свойства кривой п: интересные черты геометрии
Во-первых, кривая п обладает симметрией, что означает, что ее две половины, разделенные осью симметрии, являются зеркальными отражениями друг друга. Эта особенность делает ее весьма привлекательной для математиков и искусствоведов, которые находят в ней источник вдохновения и гармонии.
Во-вторых, кривая п обладает свойством постоянной кривизны. Это означает, что в любой ее точке радиус кривизны имеет постоянное значение. Это свойство позволяет рассматривать кривую п с точки зрения дифференциальной геометрии и использовать ее в различных приложениях, таких как проектирование мостов и архитектурных сооружений.
В-третьих, кривая п обладает неограниченной длиной. Это означает, что независимо от выбранной точки на кривой, можно найти бесконечное количество точек, принадлежащих кривой. Это свойство делает ее объектом изучения для математиков и физиков, которые исследуют ее фрактальную природу и применяют ее в хаотической динамике.
И наконец, кривая п обладает необычной связью с числом π. Длина окружности п пропорциональна ее диаметру и равна 2π. Эта связь с математической константой π делает кривую п объектом изучения в алгебре и анализе.
Изучение и определение характеристик окружности п

Определение таких характеристик, как длина окружности, диаметр, радиус и площадь, позволяет нам более полно понять и описать геометрическую природу окружности п. Длина окружности п, известная как окружность, является одним из основных параметров, от которого зависят другие характеристики. Диаметр – это отрезок, соединяющий две точки на окружности и проходящий через ее центр, в то время как радиус – это расстояние от центра до любой точки окружности. Площадь окружности рассчитывается с использованием формулы, связывающей радиус и площадь.
Изучение и определение параметров окружности п имеет важное значение во многих областях, таких как геометрия, физика, инженерия и строительство. Понимание этих характеристик позволяет нам анализировать и моделировать различные физические и геометрические явления, а также применять их в практических расчетах и построениях.
Определение положения точки на окружности: методы и их особенности
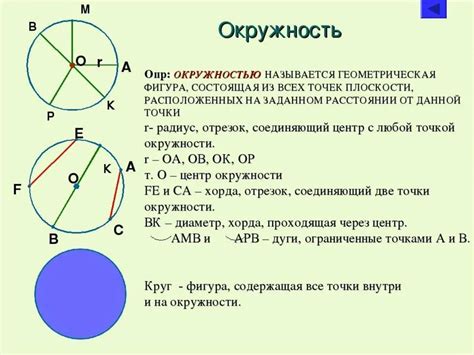
В данном разделе будут рассмотрены различные методы определения положения точки на окружности п. Каждый метод имеет свои особенности и применяется в определённых ситуациях.
- Метод геометрических построений
- Метод использования координат
- Метод использования углов
- Метод использования длин дуг
Метод геометрических построений основан на построении треугольников и конструктивных преобразованиях, позволяющих определить положение точки на окружности п. Этот метод требует точности в выполнении построений и знания основ геометрии.
Метод использования координат основан на задании окружности в декартовой системе координат и определении координат точки на окружности. При помощи вычислений и сравнения координат можно определить положение точки относительно окружности п.
Метод использования углов основан на вычислении угла между радиусом, проведенным к центру окружности, и прямой, соединяющей центр окружности с точкой на окружности п. Угол позволяет определить положение точки относительно окружности.
Метод использования длин дуг основан на измерении длин дуг окружности, а также отрезков, соединяющих центр окружности с точкой на окружности п. Путём сравнения длин дуг и прямых отрезков можно определить положение точки на окружности.
Координаты точки на окружности п
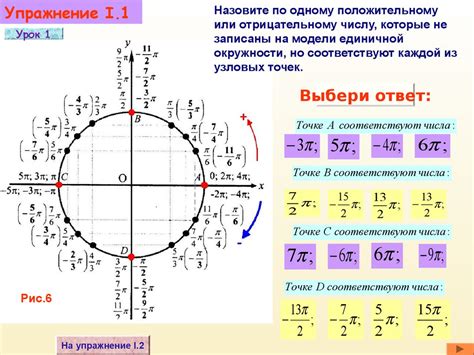
В данном разделе рассмотрим способы нахождения координат точки на окружности п, используя геометрические и тригонометрические свойства.
Для начала, рассмотрим основные понятия, связанные с окружностью и координатной плоскостью. Окружность – это геометрическое место точек, равноудаленных от фиксированной точки, называемой центром окружности. Координатная плоскость представляет собой двумерное пространство, где каждая точка имеет свои координаты, обозначающие ее положение.
Для нахождения координат точки на окружности п, необходимо знать радиус окружности и значение угла, на котором находится искомая точка. Пользуясь соответствующими формулами и формулами перевода из полярной системы координат в декартову, можно вычислить значения координат точки.
| Метод | Описание |
|---|---|
| Использование тригонометрии | Данный подход основывается на использовании тригонометрических функций (синус, косинус), а также угла, на котором находится точка на окружности. Путем применения соответствующих формул можно выразить значения координат точки. |
| Использование геометрии | Этот метод основан на геометрических свойствах окружности и построении треугольников, включающих центр окружности, радиус и искомую точку. Применение геометрических законов позволяет найти координаты точки. |
Выбор метода зависит от конкретной задачи и предпочтений исследователя. Оба подхода имеют свои преимущества и нюансы, и решение о выборе метода должно основываться на конкретных условиях задачи.
Геометрические и вычислительные методы определения координат

Раздел посвящен исследованию различных геометрических и вычислительных методов определения координат точки на плоскости. Эти методы позволяют установить точное положение объектов относительно друг друга, применяются в различных областях, таких как геодезия, навигация, компьютерное зрение и робототехника.
Одним из геометрических методов определения координат является трехгиперболический метод. Он основан на использовании гиперболических функций для определения расстояния от неизвестной точки до известных контрольных точек. Этот метод позволяет с высокой точностью определить координаты и использовать его для построения геометрических моделей и картирования местности.
Другим важным методом является использование трехмерных преобразований для определения координат. Этот метод позволяет определить положение точки в трехмерном пространстве с помощью матричных операций. Он широко применяется в компьютерной графике и компьютерном зрении для трехмерной реконструкции объектов и определения их положения в пространстве.
Также в разделе рассматривается использование интерполяции для определения координат. Интерполяция позволяет вычислить координаты точки на основе существующих данных о ближайших точках. Этот метод часто используется в геодезии, аэрофотограмметрии и картографии для восстановления пропущенных или недостоверных данных о координатах точек на местности.
| Метод | Описание |
|---|---|
| Трехгиперболический метод | Определение координат с использованием гиперболических функций и контрольных точек |
| Метод трехмерных преобразований | Определение координат в трехмерном пространстве с помощью матричных операций |
| Метод интерполяции | Определение координат на основе данных о ближайших точках |
Расчет координат точек на окружности при помощи практических примеров
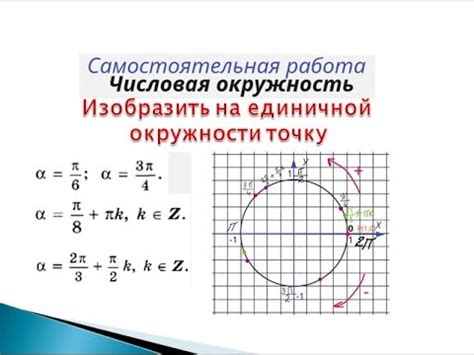
В данном разделе представлены практические примеры, которые помогут вам научиться расчитывать координаты точек на окружности п. При анализе различных ситуаций и примеров вы сможете лучше понять, как использовать полученные знания в реальной практике.
Пример 1: Расчет координат точек на окружности
Для начала давайте рассмотрим простой пример, чтобы понять, как рассчитывать координаты точек на окружности п. Предположим, что радиус окружности равен 4 единицам. Тогда мы можем использовать следующие формулы:
| Угол (в градусах) | Координата X | Координата Y |
|---|---|---|
| 0 | 4 | 0 |
| 30 | 3.464 | 2 |
| 60 | 2 | 3.464 |
| 90 | 0 | 4 |
| 120 | -2 | 3.464 |
| 150 | -3.464 | 2 |
| 180 | -4 | 0 |
| 210 | -3.464 | -2 |
| 240 | -2 | -3.464 |
| 270 | 0 | -4 |
| 300 | 2 | -3.464 |
| 330 | 3.464 | -2 |
В этом примере мы использовали формулы, основанные на тригонометрии, чтобы вычислить координаты точек на окружности п. Продолжая изучать и практиковать подобные примеры, вы получите навыки в расчетах с более сложными параметрами и сможете применить их в различных сферах, таких как геометрия, физика и программирование.
Связь окружностей и поверхностей вращения: исследование взаимодействия
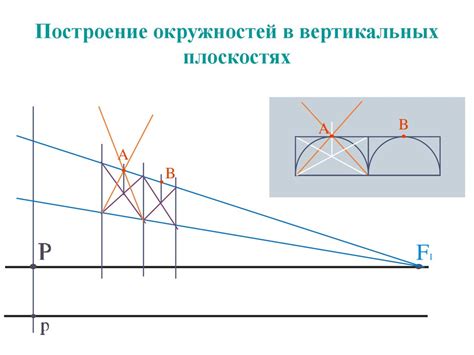
В этом разделе мы рассмотрим уникальное соотношение между фигурой, образованной окружностью п, и поверхностью вращения. Изучение этой взаимосвязи позволяет нам получить глубокое понимание форм и свойств различных объектов. За пределами конкретных определений, мы исследуем общую идею, заложенную в этой связи, анализируя и объясняя важность и применение данного концепта в различных областях знаний.
1. Вычисление площади фигуры на основе окружности п
- 1.1 Применение теоремы Пифагора для расчета площади
- 1.2 Практические примеры использования этого метода
- 1.3 Зависимость площади фигуры от радиуса окружности п
2. Формирование поверхности вращения с использованием окружности п
- 2.1 Описание и принципы формирования поверхностей вращения
- 2.2 Влияние радиуса и центра окружности п на форму поверхности
- 2.3 Примеры реальных объектов, образующих поверхности вращения на основе окружности п
3. Взаимосвязь формы окружности п и поверхности вращения
- 3.1 Исследование изменений в форме поверхности при изменении радиуса окружности п
- 3.2 Визуализация связи между окружностью п и поверхностью вращения
- 3.3 Практическое применение данной связи в архитектуре, дизайне и других областях
В этом разделе мы углубимся в изучение взаимосвязи окружности п и поверхности вращения, раскрывая их сущность и применение. Благодаря этому, вы сможете лучше понять характеристики и форму объектов, а также применять данное знание в своей деятельности.
Особенности формирования поверхностей методом вращения кривых
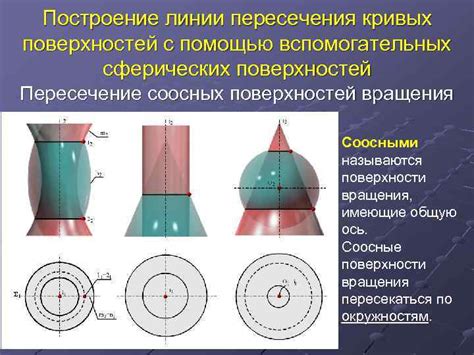
Вращение окружности, которая является одной из базовых кривых, позволяет создать особую категорию поверхностей с уникальными характеристиками. При этом, важно учитывать, что форма и свойства полученной поверхности зависят от параметров вращения, таких как радиус и скорость вращения, а также от формы и геометрии исходной кривой - окружности.
- Первое свойство, на которое следует обратить внимание - это создание поверхности в форме тора, при вращении окружности вокруг оси, параллельной плоскости окружности.
- Другое интересное явление - формирование конической поверхности, при вращении окружности вокруг одного из своих диаметров.
- Также возможно формирование сферической поверхности при вращении окружности вокруг его диаметра, лежащего в плоскости окружности.
Таким образом, поверхности, образованные вращением окружности, предоставляют широкий спектр возможностей в создании разнообразных форм и конструкций. Их использование позволяет добиться эффектных результатов в архитектуре, инженерии и дизайне, привлекая внимание своей необычностью и оригинальностью.
Вопрос-ответ

Как найти точку на окружности п, которая находится на 4 радиуса от начальной точки?
Чтобы найти точку на окружности п, которая находится на 4 радиуса от начальной точки, следует продолжить радиус путем наложения на окружность и отмерить 4 радиуса от начальной точки. Это будет координатами искомой точки.
Как определить, где на окружности п находится точка, которая отстоит от начальной точки на 4 радиуса?
Для определения положения точки на окружности п, которая отстоит от начальной точки на 4 радиуса, необходимо отложить на окружности 4 радиуса от начальной точки в направлении по часовой стрелке или против часовой стрелки. Точка, на которой они пересекут окружность, будет искомой точкой.
Как найти координаты точки на окружности п, расположенной на расстоянии 4 радиуса от начальной точки?
Для нахождения координат точки на окружности п, которая находится на расстоянии 4 радиуса от начальной точки, нужно использовать уравнение окружности и подставить вместо переменной радиуса значение 4. Это позволит найти координаты искомой точки.
Как построить точку на окружности п, которая лежит на 4 радиуса от начальной точки?
Для построения точки на окружности п, которая лежит на 4 радиуса от начальной точки, необходимо провести радиус от начальной точки и продолжить его за пределы окружности. Затем отложить на нем отрезок длиной, равной 4 радиусам. Точка пересечения этого отрезка с окружностью будет искомой точкой.