Мир науки всегда прогрессирует, открывая перед нами удивительные и неожиданные возможности. Одно из таких открытий оказалось под напряженным вниманием специалистов в области математики и логики, ставя перед ними новые вызовы и задачи
Суть этого великого открытия заключается в том, что добавление плюса в операции умножения позволяет значительно расширить нашу сознательную трансцендентность, обогатив таким образом наши мыслительные процессы. Такое новаторство вызвало смешанные эмоции среди ученых: от восторга и радости до сомнений и недоумения - все они признали, что этот феномен нельзя игнорировать и требует более детального изучения.
Новые правила: расширение возможностей сложения

В дополнение к традиционной концепции сложения, которая обозначает сочетание двух чисел для получения их суммы, существуют более глубокие и интересные подходы к этой операции.
- Сумма - не только числа: рассмотрим случаи, когда сложение применяется к нечисловым объектам, а также к абстрактным идеям.
- Игра с противоположностями: изучим, как использовать сложение для работы с противоположностями и противоположными понятиями.
- Сложение в контексте расширенной алгебры: представим новые математические системы, в которых сложение обладает свойствами, отличными от обычных.
- Синтез и композиция: изучим суть сложения как операции синтеза и композиции, позволяющей создавать новые объекты и явления.
- Расширение понятия суммы: разберемся с тем, как понимание сложения может быть расширено и применено в других областях знаний, включая философию, логику и искусство.
Эти новые правила и идеи добавляют глубину и гибкость в наше понимание сложения. Они помогают нам видеть его не просто как арифметическую операцию, а как мощный инструмент для исследования, композиции и создания новых знаний.
Умножение числа на другое число: преимущества и область применения
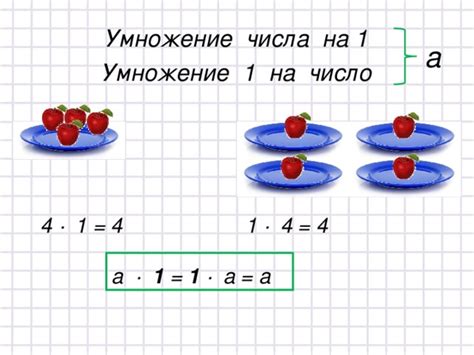
В математике существует интересный прием, который позволяет увеличить одно число за счет другого числа. Этот метод дает возможность добиться более высокой степени прироста и разнообразия, позволяя нам расширить понимание и применение умножения.
Умножение числа на другое число является мощным инструментом, которое позволяет получить дополнительные ресурсы, повысить результативность и добиться лучшего результата. Это подход, который позволяет использовать уже имеющиеся ресурсы в умелом сочетании, с целью достижения большей эффективности и роста. Главное преимущество этого метода заключается в том, что он позволяет нам оперировать не только с изначальным числом, но и с его умножением на другое число, что значительно расширяет возможности и вероятности для достижения поставленных целей.
Применение умножения числа на другое число может быть использовано в разных областях. В экономике этот метод позволяет увеличить прибыльность бизнеса, за счет рационального распределения ресурсов и оптимального использования факторов производства. В науке он дает нам возможность модифицировать и усовершенствовать уже существующие процессы, повышая эффективность и результативность исследований. В повседневной жизни этот подход может быть использован для достижения личных целей, развития навыков и повышения качества жизни в целом.
В результате, понимание и активное использование умножения числа на другое число дает нам возможность обогатить наши знания и опыт, расширить границы нашего мышления и достичь больших успехов в различных аспектах жизни, от профессиональной деятельности до личного развития.
Умножение положительных чисел: за и против
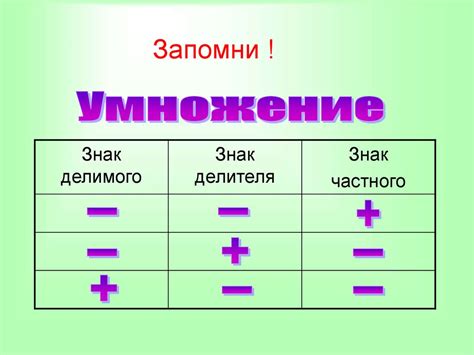
Прежде чем перейти к анализу, стоит отметить, что умножение положительных чисел – важный аспект в математике, который находит широкое применение в повседневной жизни и различных профессиональных областях. Плюсы и минусы данной операции могут быть весьма значимыми при решении задач и принятии решений.
| Преимущества | Недостатки |
|---|---|
| Позволяет увеличивать значение числа в несколько раз | Не подходит для отрицательных чисел |
| Облегчает расчеты и сокращает время выполнения задач | Может привести к потере точности при умножении больших чисел |
| Используется в экономических и финансовых расчетах | Требует времени и усилий для выполнения умножения вручную |
Подводя итог, умножение положительных чисел имеет свои достоинства и ограничения. Оно является полезным инструментом в решении разнообразных задач и может значительно упростить расчеты. Однако, необходимо учитывать его ограничения и возможные потери точности при работе с большими числами.
Отрицательные числа: новый подход к результату умножения

Умножение отрицательных чисел вызывает особый интерес и может быть представлено с использованием нового подхода к сложению. Этот метод позволяет найти результат умножения отрицательных чисел без прямого участия операции умножения.
Использование нового подхода:
Для понимания нового подхода к умножению отрицательных чисел нужно обратиться к концепции сложения. Результат умножения двух чисел можно представить как сумму множителей, при этом одно из чисел может быть отрицательным. В контексте нового подхода отрицательное число можно рассматривать как изменение значения начального числа в отрицательную сторону. Таким образом, при умножении отрицательных чисел мы можем рассматривать операцию как сложение измененных значений.
Пример использования нового подхода:
Представим, что нам нужно умножить -3 на -2. Для этого мы можем рассмотреть операцию как сумму -3 и -3 с учетом изменения знака. Изначально значение -3 имеет отрицательный знак, а после изменения становится положительным, добавляется другое -3, также со знаком изменения, которое преобразуется в положительное значение. Итоговая сумма будет равна 6, так как дважды учтены изменения знака числа -3.
Заключение:
Разработка нового подхода к умножению отрицательных чисел позволяет упростить вычисления и получить точные результаты. Этот подход позволяет рассматривать умножение отрицательных чисел как сложение измененных значений, что значительно расширяет наше понимание математических операций.
Понятие умножения на отрицательное число: ключевые моменты
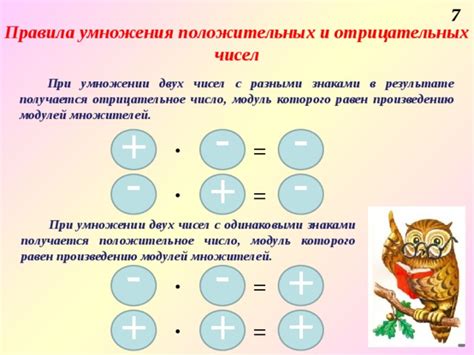
Когда мы умножаем два положительных числа, результат будет положительным числом. Но что происходит, когда одно из чисел отрицательное? Здесь появляется необходимость понимания ключевых моментов умножения на отрицательное число.
Ключевой момент №1: Умножение отрицательного числа на положительное
Если у нас есть отрицательное число и положительное число, то результат умножения будет отрицательным. Например, (-2) * 3 = -6. В таких случаях отрицательное число "меняет знак" и становится положительным, а затем перемножается с положительным числом.
Ключевой момент №2: Умножение отрицательного числа на отрицательное
Если мы умножаем два отрицательных числа, то результат умножения будет положительным числом. Например, (-2) * (-3) = 6. В этом случае, оба числа "меняют знак" и становятся положительными, а затем перемножаются. Это правило является следствием расширения понятия умножения.
Ключевой момент №3: Приоритет отрицательного числа
Важно понимать, что в умножении на отрицательное число, отрицательность имеет приоритет над операцией умножения. Например, -3 * 4 не равно 12, а равно -12. Это значит, что отрицательное число "перекрывает" операцию умножения и сохраняет свой знак.
Теперь, зная эти ключевые моменты, мы можем более точно работать с умножением на отрицательное число и получать правильные результаты в математических выражениях.
Кратность и умножение: получение конечного результата

В этом разделе мы рассмотрим методы определения конечного результата при умножении чисел, основываясь на понятии кратности. В процессе умножения чисел мы будем исследовать, каким образом можно получить итоговое значение, используя различные подходы и принципы.
Кратность – это свойство чисел, которое определяет, сколько раз одно число содержится в другом числе без остатка. Например, число 6 содержится в числе 18 три раза без остатка, поэтому говорят, что 6 является кратным числом для 18.
Кратность и умножение тесно связаны друг с другом: для получения результата умножения двух чисел, мы можем разложить одно из чисел на сумму кратных ему чисел, а затем умножить каждое кратное на другое число. Таким образом, мы расширяем понимание умножения и используем принципы кратности для получения итогового значения.
В следующих разделах мы рассмотрим конкретные способы использования кратности при умножении чисел и приведем примеры, которые помогут наглядно представить этот процесс. По окончании чтения статьи вы поймете, как определить результат умножения чисел, используя принципы кратности, и сможете применить эти знания на практике.
Продолжительность движения вперед, определяемая масштабом умножения положительного числа на отрицательное

Итоговые значения при умножении положительного числа на отрицательное могут принести неожиданные результаты, связанные с изменением направления движения. Здесь мы рассмотрим положительное число в качестве изначального пути и отрицательное число в качестве множителя. Возникает вопрос: каковы будут итоговые значения, когда два противоположных направления объединяются при умножении?
Положительное число, на первый взгляд, указывает на продолжение движения вперед. Отрицательное число, напротив, предполагает движение в обратном направлении. Если мы умножаем положительное число на отрицательное, становится интересно, как сочетание этих противоположных величин влияет на конечную точку пути.
Результатом умножения положительного числа на отрицательное является отрицательное число. Это указывает на изменение направления движения и приостановление продвижения вперед. Таким образом, положительное число и отрицательное число сливаются вместе, чтобы сформировать итоговое значение, противоположное исходному пути. В конечном итоге, движение вперед превращается в движение назад.
Складывая произведения: методы и примеры

Метод сложения умноженных чисел в теории чисел:
Первый метод, который мы рассмотрим, основан на важных принципах теории чисел. Путем суммирования произведений действительных чисел, мы можем обнаружить интересные закономерности, связанные с арифметическими операциями. В этой статье мы исследуем принципы метода и предоставим примеры его применения.
Сложение произведений с использованием паттернов:
Второй метод позволяет использовать паттерны для сложения умноженных чисел. Мы представим несколько примеров паттернов, которые помогут вам легче понять, как складывать такие числовые выражения. Этот метод особенно полезен при работе с большими числами и при решении сложных математических задач.
Примеры сложения умноженных чисел:
В третьей части статьи мы представим реальные примеры, в которых мы будем складывать числа, предварительно умноженные друг на друга. Вы увидите, как эти примеры могут быть использованы в практических задачах и как они расширяют наше понимание операции сложения. Это поможет вам лучше овладеть этой темой и применить полученные знания в дальнейшей работе.
В этом разделе мы рассмотрели методы и примеры сложения умноженных чисел, которые позволяют нам расширить понимание операции сложения и применять его к новым числовым выражениям. Различные методы и примеры помогут вам научиться более глубоко анализировать и решать математические задачи, связанные с этой темой.
Отрицательное число добавляется к положительному: обобщение плюса

В этом разделе мы рассмотрим интересный аспект математической операции, связанной с суммированием чисел. Когда мы добавляем отрицательное число к положительному, происходит обобщение понятия "плюс".
Этот процесс позволяет нам расширить наше понимание о том, как два числа могут объединяться, внося при этом определенные изменения в результат. Используя данную операцию, мы можем оценивать и вычислять различные ситуации, где взаимодействуют числа с разным знаком. Это важно, так как нам дает возможность работать с более широким спектром числовых значений и решать разнообразные задачи.
- Экспериментируем с отрицательными числами: решение задач на добавление отрицательного числа к положительному.
- Изучаем особенности взаимодействия чисел с противоположными знаками: описание результатов добавления.
- Применяем обобщенное понятие плюса в практических задачах, где нужно учитывать разные комбинации положительных и отрицательных чисел.
- Рассматриваем примеры из реальной жизни, где использование обобщенного плюса помогает нам сделать точные расчеты и принять рациональные решения.
В результате изучения этого раздела вы сможете применять обобщенное понятие "плюс" при добавлении отрицательного числа к положительному и применять полученные знания в практических ситуациях. Это расширит ваши математические навыки и поможет вам более гибко и эффективно обрабатывать разнообразные задачи, где важны значения чисел с разными знаками.
Умножение нуля на произвольное число: особенности и решения

Уникальная ситуация: рассмотрим случай, когда наше произвольное число умножается на ноль. Это особенное умножение имеет свои закономерности и может привести к некоторым необычным результатам.
Решение 1: Свойство абсорбции
В математике существует понятие абсорбции, которое гласит, что умножение числа на ноль равно нулю: если умножить любое число на ноль, то результатом всегда будет ноль.
Например, 0 умножить на любое число, будь то положительное или отрицательное, равно нулю. Это свойство значительно упрощает вычисления и иногда может использоваться для оптимизации задач.
Решение 2: Геометрическая интерпретация
Кроме абсорбции, умножение нуля на произвольное число может быть интерпретировано геометрически. Если рассмотреть числа как координаты на плоскости, то умножение на ноль означает, что точка перемещается на ось, проходя через начало координат.
Такая геометрическая интерпретация может быть полезна при решении геометрических задач и позволяет лучше понять влияние умножения на ноль на расположение точек.
Умножение положительных и отрицательных чисел: примеры из жизни

В этом разделе мы рассмотрим интересные примеры из реальной жизни, которые помогут нам лучше понять, как выполнять умножение положительных и отрицательных чисел. Мы рассмотрим ситуации, где умножение таких чисел может оказаться полезным, а также рассмотрим, какие изменения происходят при умножении, в зависимости от знаков исходных чисел.
| Пример | Описание |
|---|---|
| Умножение долга на проценты | В жизни часто возникают ситуации, когда человек имеет долг и должен выплатить проценты за пользование этим долгом. Если долг положительный, то умножение его на положительные проценты приведет к увеличению суммы долга, а если проценты отрицательные, то долг будет сокращаться. Таким образом, умножение положительных и отрицательных чисел может использоваться для расчета изменения суммы долга в зависимости от процентной ставки. |
| Умножение температуры на коэффициент | При изучении погоды и климата мы сталкиваемся с понятием коэффициента теплопроводности, который может быть как положительным, так и отрицательным. Умножение температуры на такой коэффициент позволяет определить, как будет изменяться теплопередача в материале. Если коэффициент положительный, то с ростом температуры будет увеличиваться теплопередача, а если коэффициент отрицательный, то теплопередача будет уменьшаться. |
| Умножение прибыли на стоимость товара | В коммерческой деятельности умножение положительных и отрицательных чисел также является распространенной операцией. Например, чтобы определить общую прибыль от продажи определенного количества товаров, необходимо умножить прибыль на стоимость каждого товара. Если прибыль положительная, то общая прибыль тоже будет положительной. Однако, если прибыль отрицательная, то умножение ее на положительное значение стоимости товара приведет к получению отрицательной общей прибыли. |
Такие примеры дают представление о том, как умножение положительных и отрицательных чисел применяется на практике и какие изменения происходят в зависимости от знаков исходных чисел. Использование таких операций позволяет более точно моделировать различные ситуации и сделать более точные расчеты в реальной жизни.
Вопрос-ответ

Каким образом можно расширить понятие сложения?
В математике существуют различные способы расширения понятия сложения. Один из них - использование плюса на плюс при умножении.
Что означает "плюс на плюс при умножении"?
Плюс на плюс при умножении - это специальное свойство, при котором при умножении двух положительных чисел результат будет положительным.
Как это свойство применяется в практических задачах?
Плюс на плюс при умножении может быть полезным, например, при решении задач, связанных с увеличением количества объектов или повторением определенных действий.
Существуют ли другие способы расширения понятия сложения в математике?
Да, в математике существует несколько способов расширения понятия сложения, такие как введение отрицательных чисел, операции с дробями и рациональными числами, ввод комплексных чисел и др.



