Геометрия – это волшебный мир, который кажется нам так привычным и одновременно загадочным. В нем правят законы пространства и формы, омраченные лишь одним вопросом: "Как установить равенство векторов BC и AD в квадрате ABCD?". Это замечательное отношение обнаруживает глубокую внутреннюю связь между этими двумя векторами и открывает перед нами потрясающие горизонты понимания истины в геометрии.
Равенство векторов BC и AD в квадрате ABCD – это больше, чем просто совпадение направления и длины данных векторов. В нем скрыто множество тайн, которые мы можем раскрыть, проникнув в самую суть геометрического пространства и его законов. Это особое соотношение величин, которое не оставляет равнодушными тех, кто стремится погрузиться в глубины геометрии и понять ее каноны.
Разрушая шаблоны и устоявшиеся представления, равенство векторов BC и AD взывает к нашей интуиции, аналитическому мышлению и к тому ощущению гармонии, которое возникает внутри нас при наблюдении за элегантными геометрическими конструкциями. Это не только демонстрация математической точности, но и искусство научных открытий, которое сопровождается азартом и удивлением открытых горизонтов.
Соответствие отрезков BC и AD в квадрате ABCD
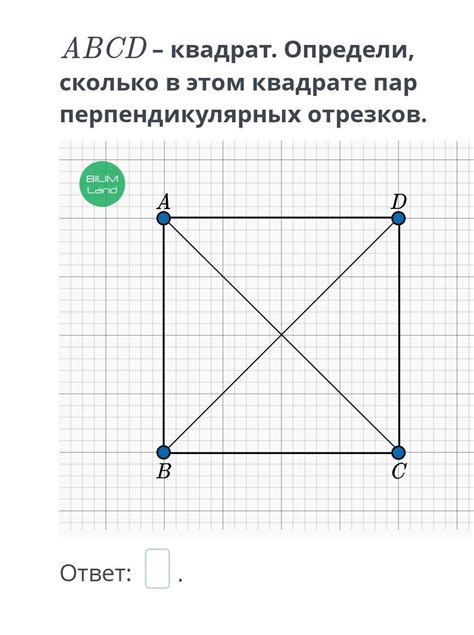
В данном разделе будет рассмотрено важное свойство, которое возникает при рассмотрении отрезков BC и AD в геометрической фигуре квадрат. Мы изучим особенности соотношений между указанными отрезками и выясним, какое влияние они оказывают на геометрические свойства квадрата.
Первоначально будет произведен анализ геометрической структуры квадрата и определение его основных элементов. Затем мы рассмотрим связь между отрезками BC и AD, и на основе этих данных выведем соответствующие заключения о равенстве данных отрезков.
| Этап | Описание |
|---|---|
| Этап 1 | Анализ геометрических свойств квадрата |
| Этап 2 | Определение отрезков BC и AD в контексте квадрата |
| Этап 3 | Исследование соотношений между отрезками BC и AD |
| Этап 4 | Доказательство равенства отрезков BC и AD |
| Этап 5 |
В результате прохождения всех указанных этапов, мы сможем более полно понять свойства и особенности квадрата, а также заключить о равенстве отрезков BC и AD и его влиянии на геометрические конструкции.
Определение векторов BC и AD
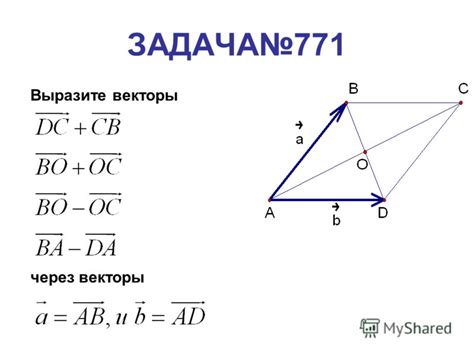
В данном разделе мы рассмотрим характеристики и свойства двух векторов, которые идентифицируются как вектор BC и вектор AD. Эти векторы описывают определенные направления и длины, которые могут быть представлены геометрически на плоскости.
Вектор BC указывает направление и расстояние от точки B до точки C на плоскости, в то время как вектор AD определяет направление и расстояние от точки A до точки D. Изучение этих векторов позволяет нам лучше понять геометрические характеристики и отношения между различными элементами в квадрате.
Вектор BC и вектор AD могут быть представлены с помощью стрелок, указывающих их направление и длину. Направление вектора обозначает движение от одной точки к другой, а его длина представляет собой величину расстояния между этими точками.
Определение и изучение этих векторов позволяет нам анализировать их свойства, такие как равенство, суммирование, разность и умножение на скаляр. Эти операции позволяют нам решать задачи, связанные с перемещением и изменением положения объектов на плоскости.
Постановка задачи о совпадении направлений линейных отрезков в фигуре
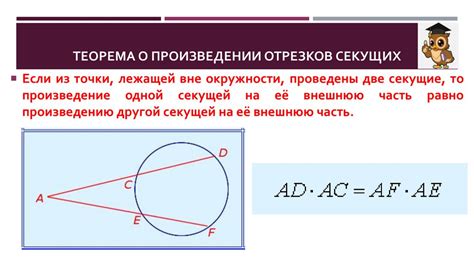
В данном разделе мы рассмотрим задачу о сопоставлении направлений линейных отрезков в геометрической фигуре, которая состоит из четырех точек. При изучении равенства векторов в данном контексте, мы будем идентифицировать отрезок вектора как длину и направление от начальной точки к конечной точке. Необходимо провести анализ относительного расположения линейных отрезков в фигуре, чтобы установить, совпадают ли их направления и, следовательно, равны ли соответствующие векторы.
| Условия задачи | Цель |
|---|---|
- Фигура состоит из четырех точек, которые можно обозначить как A, B, C и D. - Необходимо определить направления линейных отрезков BC и AD в этой фигуре. | - Установить, совпадают ли направления отрезков BC и AD в фигуре. - Пронаблюдать, равны ли соответствующие векторы. |
Для решения данной задачи важно учесть, что направление вектора описывается его ориентацией от начальной точки к конечной точке. Поэтому векторы BC и AD будут равны, если их направления совпадают и они имеют одинаковую длину. Мы будем использовать геометрические методы и концепции для анализа данной фигуры и определения соответствующих векторов с целью доказательства равенства.
Доказательство равенства линий BC и AD

В данном разделе мы рассмотрим методы и приемы, позволяющие доказать равенство линий BC и AD в геометрии. Мы используем геометрические свойства и отношения между линиями и точками, чтобы представить убедительные аргументы в пользу равенства данных линий.
Во-первых, мы рассмотрим основные понятия и определения, которые необходимы для понимания доказательства равенства линий BC и AD. Затем мы приведем примеры конкретных ситуаций, где возникает такая необходимость в доказательстве. Мы используем методы сравнения длин, углов и расстояний между точками, чтобы построить убедительную цепочку аргументов.
Важным этапом в доказательстве равенства линий BC и AD является использование свойств и отношений векторов. Мы применяем понятия направленных отрезков и операции сложения векторов, чтобы показать, что два вектора BC и AD равны. Рассмотрение свойств суммы векторов и доказательство ассоциативности этой операции имеют ключевое значение в нашем исследовании.
Наша цель - не только показать возможность доказательства равенства линий BC и AD, но и объяснить принципы и методы, лежащие в основе этого процесса. Мы пытаемся установить связь между геометрическими абстракциями и конкретными объектами, чтобы представить доказательство в наиболее понятной и наглядной форме.
Свойства квадрата ABCD в геометрии
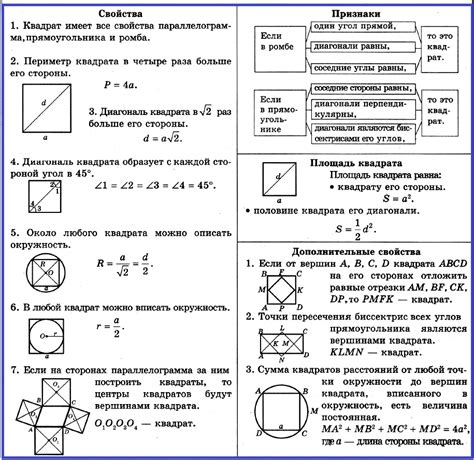
- Равенство длин сторон: в квадрате ABCD все стороны равны друг другу.
- Прямые углы: у каждого угла квадрата ABCD равная мера - 90 градусов.
- Диагонали: диагонали квадрата ABCD равны друг другу и пересекаются под прямым углом.
- Симметрия: относительно любой диагонали квадрата ABCD он симметричен.
Эти свойства делают квадрат ABCD удобным объектом для решения различных задач в геометрии. Знание данных свойств позволяет применять определенные правила и методы для доказательства равенства векторов и других геометрических соотношений в квадрате ABCD и его элементах.
Применение алгебраических методов

В данном разделе мы рассмотрим, как алгебраические методы могут быть применены для исследования и доказательства равенства векторов в геометрии. Алгебраический подход предоставляет нам инструменты для анализа и работы с векторами, основанными на их алгебраических свойствах и операциях.
Мы начнем с рассмотрения основных определений и свойств векторов, таких как коммутативность сложения и умножения на скаляр, а также ассоциативность и дистрибутивность операций. Эти свойства позволяют нам проводить алгебраические преобразования с векторами и упрощать выражения.
Затем мы рассмотрим алгебраические методы для работы с равенством векторов. Мы изучим, как применять алгебраические операции к векторам, чтобы установить или опровергнуть их равенство. Будут рассмотрены методы сокращения, сложения и вычитания векторов, а также умножения на скаляр и векторное произведение.
Далее мы познакомимся с использованием систем уравнений в алгебраическом доказательстве равенства векторов. Методы решения систем уравнений позволяют нам определить значения неизвестных векторов и проверить, равны ли они друг другу. Мы изучим как метод преобразования координат и метод компонентных равенств могут быть применены для этой цели.
- Внутри этого раздела мы рассмотрим следующие темы:
- Основные свойства векторов
- Алгебраические операции с векторами
- Методы доказательства равенства векторов
- Использование систем уравнений
- Преобразование координат и компонентные равенства
Визуальное подтверждение эквивалентности отрезков BC и AD в геометрии

Для начала рассмотрим аналогию между отрезками и силами: если мы имеем две силы, которые действуют в одном направлении и имеют одинаковые величины, то мы можем сказать, что они равны. Аналогично, отрезки BC и AD будут эквивалентными, если они одинаковы по длине и направлены в одной и той же точке.
Представим себе парусное судно на море, где мачта является главной опорой. Рассмотрим два стержня, один из которых соединен с верхушкой мачты, а другой - с одним из точек на поверхности корпуса судна. Если считать эти стержни отрезками, то можно увидеть, что они имеют одинаковую длину и направлены в главную точку на судне.
Таким образом, визуальное понимание эквивалентности отрезков BC и AD в геометрии позволяет нам увидеть, что они являются равными без необходимости вводить формальные определения и доказательства.
Ослабление условий для равенства векторов BC и AD в квадрате ABCD
В предыдущем разделе мы доказали, что векторы BC и AD равны между собой в квадрате ABCD, при условии определенного равенства. Однако, существуют случаи, когда это условие не выполняется, но векторы BC и AD все равно оказываются равными друг другу.
В данном разделе мы рассмотрим такие ситуации, где равенство векторов BC и AD возможно без выполнения предыдущего условия. Будут рассмотрены примеры, которые позволят лучше понять особенности равенства векторов в геометрии и расширить наше понимание данной концепции.
- Пример 1: Равенство векторов BC и AD при совпадении углов
- Пример 2: Равенство векторов BC и AD при одинаковых длинах сторон
- Пример 3: Равенство векторов BC и AD при одинаковых направлениях сил
Исследование данных примеров позволит нам увидеть, что равенство векторов BC и AD в геометрии имеет более широкий смысл, чем сразу может показаться.
Примеры из реальной жизни, где применяется согласованность направления движения и скорости

Например, в сельском хозяйстве фермеры избегают "дрейфа" векторов, когда нужно направить движение стада скота по определенному пути. Применяя подход равных и противоположных векторов, фермеры контролируют и поддерживают единое направление движения скота.
Аналогично, при разработке транспортных систем и инфраструктуры, инженеры учитывают согласованность направления движения транспортных средств. Например, на развязках и перекрестках дорог, правильное понимание равенства векторов позволяет создать безопасные пути движения автомобилей, предотвращая аварии и улучшая поток транспорта.
Также, в физике равенство векторов играет важную роль при изучении движения тел и рассмотрении сил, действующих на них. Согласованность и равенство векторов могут помочь в предсказании траекторий объектов и объяснении поведения материальных тел в различных условиях.
Эти наглядные примеры показывают, что равенство векторов не является просто абстрактным понятием, применимым только в геометрии. Используя согласованность направления движения и скорости, мы можем достичь более эффективного и безопасного функционирования в различных областях деятельности.
Вопрос-ответ

Как можно доказать равенство векторов BC и AD в квадрате ABCD в геометрии?
Доказать равенство векторов BC и AD в квадрате ABCD можно применив определение равенства векторов. Сначала нужно найти координаты векторов BC и AD, затем сравнить их координаты и убедиться, что они равны. Если координаты векторов BC и AD совпадают, то можно сделать вывод, что эти векторы равны друг другу.
Какой смысл имеет равенство векторов BC и AD в квадрате ABCD?
Равенство векторов BC и AD в квадрате ABCD означает, что эти векторы имеют одинаковую длину и направление. Это, в свою очередь, означает, что сторона BC квадрата ABCD равна стороне AD и направлена в том же направлении. Такое равенство векторов позволяет сделать вывод о симметрии и равенстве квадрата ABCD.
Какие свойства векторов можно использовать для доказательства равенства BC и AD в квадрате ABCD?
Одно из свойств векторов, которое можно использовать для доказательства равенства BC и AD в квадрате ABCD, это свойство суммы векторов. Если вектор AB равен вектору AC, то можно сказать, что вектор BC равен вектору AD. Это свойство позволяет применить транзитивность равенства и сделать вывод о равенстве векторов BC и AD.
Каким образом равенство векторов BC и AD в квадрате ABCD может быть использовано в практических задачах геометрии?
Равенство векторов BC и AD в квадрате ABCD может быть использовано для решения различных задач геометрии. Например, если известны координаты векторов BC и AD, то с их помощью можно найти координаты других векторов квадрата ABCD или рассчитать длину сторон и диагоналей квадрата. Также равенство векторов BC и AD может быть использовано для доказательства других геометрических свойств, например, симметрии квадрата относительно его диагоналей.



