Мир, окружающий нас, сложен и непредсказуем. Все процессы проходят через небывалое многообразие изменений, и каждое из них имеет свои законы. Однако, не всегда эти законы могут быть описаны простыми словами или общепринятыми формулами. В некоторых случаях, чтобы получить истинное представление о процессе или явлении, нам необходимо использовать математический аппарат, а именно - дифференциальные уравнения.
Дифференциальные уравнения являются мощным инструментом, который помогает нам понять сложные процессы в нашем мире. Они позволяют выразить изменение, скорость и взаимосвязь между различными переменными в виде математических соотношений. С помощью дифференциальных уравнений мы можем предсказывать будущие значения переменных, анализировать стабильность системы, определять точки перегиба или экстремумы функций.
Применение дифференциальных уравнений затрагивает такие различные области, как физика, экономика, биология и даже медицина. В физике, они позволяют описывать движение тел, изменение температуры, распространение волн и другие физические явления. В экономике, дифференциальные уравнения используются для моделирования экономических процессов, позволяя предсказывать очень сложные и нелинейные системы. В биологии дифференциальные уравнения применяются для описания популяционных моделей, включая изменение численности видов, взаимодействие между видами и т.д. А в медицине, дифференциальные уравнения используются для описания распространения заболеваний, динамики лекарственных препаратов в организме, а также для анализа эффективности лечения.
Расчет траектории полета ракеты с применением дифференциальных уравнений
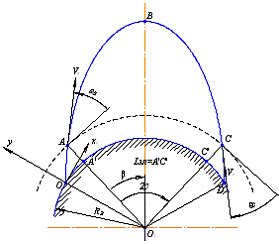
Путешествие космической ракеты начинается с ее запуска с поверхности Земли и заканчивается достижением целевой орбиты или другого назначенного космического объекта. Это сложная задача, которая требует точных расчетов и предсказаний движения ракеты в космическом пространстве. Для этого используются дифференциальные уравнения, которые описывают изменение скорости и положения ракеты во времени.
Одной из основных задач расчета траектории полета ракеты является определение пути, который она должна пройти, и оптимального момента для включения двигателя и его выключения. Дифференциальные уравнения позволяют предсказать, как ракета будет двигаться в зависимости от силы тяги двигателя, сопротивления воздуха и гравитационного притяжения Земли.
При расчете траектории полета ракеты задачей является решение системы дифференциальных уравнений, в которых учитываются взаимодействия между различными физическими параметрами. Например, уравнения движения ракеты могут учитывать изменение массы ракеты с течением времени из-за сгорания топлива, а также изменение силы тяги и сопротивления воздуха.
Использование дифференциальных уравнений при расчете траектории полета ракеты позволяет учесть множество факторов, которые влияют на ее движение. Это позволяет разработчикам оптимизировать траекторию полета и достичь требуемой орбиты с минимальными затратами топлива. Также эти расчеты важны для безопасности полета и предотвращения столкновений с другими космическими объектами.
Использование физических законов для моделирования движения

В данном разделе мы рассмотрим, как физические законы могут быть применены для создания математических моделей, которые описывают движение объектов в реальном мире. Эти модели основываются на дифференциальных уравнениях, которые описывают изменение параметров объекта с течением времени. Используя эти уравнения, мы можем предсказать траекторию и скорость движения объектов, а также оценить другие важные характеристики и свойства.
Чтобы создать подобные модели, нам необходимо учитывать различные физические законы, такие как законы Ньютона, закон сохранения энергии и закон сохранения момента импульса. В зависимости от конкретной задачи, мы выбираем соответствующий закон и применяем его к нашей модели.
Одним из примеров использования дифференциальных уравнений для моделирования движения является задача броска предмета под углом. С помощью закона баллистики и уравнений движения, мы можем определить траекторию полета объекта, его максимальную высоту и дальность полета.
Еще одним примером является моделирование движения тел на плоскости под воздействием силы трения. Используя уравнения Ньютона и уравнения движения, мы можем определить скорость, ускорение и положение объекта в конкретный момент времени.
- Моделирование движения планет вокруг Солнца с помощью закона всемирного тяготения
- Исследование колебаний математического маятника с использованием уравнения гармонических колебаний
- Определение траектории и скорости ракеты в атмосфере с использованием уравнений Навье-Стокса
- Моделирование движения жидкости в трубе с помощью уравнения Навье-Стокса
Моделирование динамики популяции через применение дифференциальных уравнений

Процессы роста и снижения популяций являются сложными и динамическими. Они зависят от многих факторов, таких как рождаемость, смертность, миграция, конкуренция за ресурсы и влияние окружающей среды. Чтобы понять и предсказать динамику популяции, мы используем дифференциальные уравнения для моделирования этих процессов.
Моделирование популяционной динамики позволяет:
- Изучить рост и устойчивость популяции: Дифференциальные уравнения позволяют нам проанализировать, как изменения в различных факторах влияют на рост или уменьшение численности популяции. Мы можем определить, какие факторы являются ключевыми для поддержания стабильной популяции и предотвращения ее коллапса.
- Предсказать будущие изменения: Моделирование популяционной динамики позволяет нам предугадать, как изменения в окружающей среде или других факторах могут повлиять на популяцию в будущем. Это может быть полезно для принятия мер по устранению или смягчению негативных воздействий.
- Оценить эффективность мер по управлению популяцией: Моделирование популяционной динамики позволяет нам оценить результаты примененных мер по управлению популяцией. Мы можем предсказывать, какие стратегии будут более эффективными для сохранения или регулирования численности популяции в конкретных ситуациях.
Моделирование популяционной динамики с использованием дифференциальных уравнений является мощным инструментом для изучения и понимания сложных процессов, происходящих в живых организмах. Оно позволяет нам получить более глубокий и точный анализ взаимодействий в популяциях и разработать эффективные стратегии управления и сохранения биоразнообразия.
Решение задачи прогнозирования изменений численности популяции
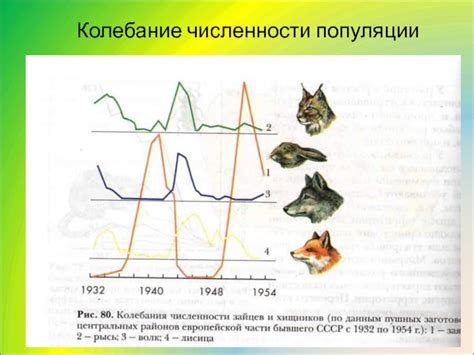
В данном разделе рассмотрим применение дифференциальных уравнений для решения задачи прогнозирования изменений численности популяции различных организмов. Чтобы предсказать будущее состояние популяции, необходимо учитывать различные факторы, влияющие на ее изменение, такие как рождаемость, смертность, миграция и взаимодействие с другими популяциями.
Дифференциальные уравнения позволяют описать эти изменения в виде математической модели, которая может быть использована для прогнозирования динамики популяции в будущем. Принцип такой модели заключается в представлении изменения численности популяции как производной от времени.
- Рождаемость может быть описана дифференциальным уравнением, учитывающим прирост числа особей в популяции;
- Смертность может быть представлена уравнением, учитывающим убыль популяции в результате естественных и других факторов;
- Миграция может быть учтена через дифференциальное уравнение, отражающее переселение особей из одной популяции в другую;
- Взаимодействие с другими популяциями может быть учтено через системы дифференциальных уравнений, описывающих взаимодействие между популяциями разных видов.
Используя эти дифференциальные уравнения, можно прогнозировать будущую численность популяции, а также изучать влияние различных факторов на ее динамику. Такой подход позволяет провести анализ и принять меры для сохранения и эффективного управления популяциями различных организмов в реальных условиях.
Прогноз погоды на основе математических моделей

Прогноз погоды на основе дифференциальных уравнений основывается на представлении атмосферы как сложной системы, подчиняющейся определенным физическим законам. В такой модели уравнения, описывающие распространение атмосферных параметров в пространстве и времени, играют роль основного инструмента для прогнозирования погоды. Эти уравнения учитывают множество факторов, таких как солнечная радиация, конвекция, влияние океанов и многое другое, что позволяет более точно оценить будущие изменения погодных условий.
- Дифференциальные уравнения используются для моделирования изменений атмосферных параметров в пространстве и времени.
- Точное решение дифференциальных уравнений позволяет предсказывать погоду с высокой точностью.
- Прогноз погоды на основе дифференциальных уравнений используется метеорологическими службами для предупреждения о неблагоприятных погодных условиях, таких как сильные ливни, ураганы или засухи.
- Математические модели на основе дифференциальных уравнений позволяют ученым изучать долгосрочные паттерны климатических изменений и предсказывать их последствия.
Прогноз погоды на основе дифференциальных уравнений является наиболее точным и надежным методом, который позволяет получить полное представление о будущих погодных условиях. Этот подход применяется в мировой метеорологии и играет важную роль в обеспечении безопасности и комфорта жизни людей во всем мире.
Анализ данных о температуре, влажности и давлении для предсказания погодных условий
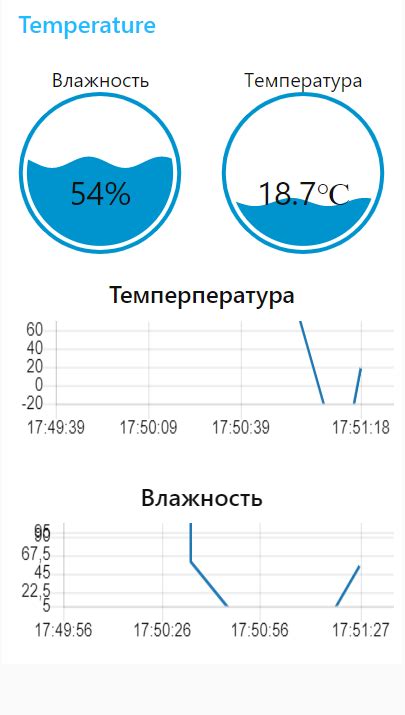
Дифференциальные уравнения играют важную роль в моделировании погодных явлений. Они позволяют учесть сложную динамику взаимодействия температуры, влажности и давления, а также других факторов, которые влияют на погоду.
Данные о температуре, влажности и давлении собираются с помощью метеостанций, радиозондов, спутников и других приборов, расположенных в различных точках планеты. После сбора, эти данные анализируются и обрабатываются с использованием дифференциальных уравнений и других методов статистического анализа.
| Параметр | Описание | Единицы измерения |
|---|---|---|
| Температура | Измерение количества теплоты воздуха | градус Цельсия |
| Влажность | Отношение количества водяного пара в воздухе к максимально возможному | процент |
| Давление | Сила, с которой атмосфера действует на поверхность | гектопаскаль |
Данные о температуре, влажности и давлении анализируются с использованием различных дифференциальных уравнений, таких как уравнения теплопроводности, уравнения движения воздуха и уравнения влажности. Эти уравнения учитывают как локальные, так и глобальные факторы, такие как солнечная радиация, ветер и географические особенности местности.
Результаты анализа позволяют предсказать погодные условия на определенный период времени. Это важно для различных отраслей, таких как сельское хозяйство, авиация, строительство и туризм. На основе данных о температуре, влажности и давлении можно принимать решения о поливе растений, планировании полетов и определении оптимальных условий строительства.
Оптимальное управление движением робота с применением дифференциальных уравнений
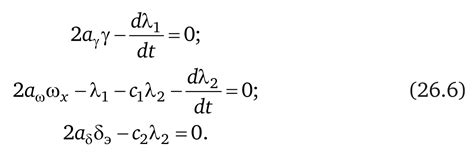
В данном разделе рассмотрим применение дифференциальных уравнений для достижения оптимального управления движением робота. Роботы стали неотъемлемой частью нашей современной жизни, выполняя различные задачи в автоматизированных системах. Однако, для эффективного функционирования роботов, необходимо разработать методы управления, которые помогут им эффективно перемещаться и выполнять различные задачи.
Технический прогресс в области робототехники позволяет создавать все более сложные и гибкие роботы. Однако, движение роботов может быть ограничено различными факторами, такими как геометрические ограничения пространства, физические ограничения самого робота или ограничения на время выполнения задачи. Чтобы оптимизировать движение робота, можно использовать дифференциальные уравнения, которые описывают зависимость координат и скоростей робота от времени.
| Преимущества применения дифференциальных уравнений: |
|---|
| 1. Возможность моделирования и предсказания движения робота в различных условиях и сценариях. |
| 2. Учёт ограничений и оптимизации параметров движения, таких как скорость и траектория. |
| 3. Гибкость и адаптивность системы управления роботом для решения разнообразных задач с учетом условий окружающей среды. |
| 4. Возможность управления роботом в режиме реального времени, обеспечивая высокую точность и плавность движения. |
Применение дифференциальных уравнений в управлении движением робота позволяет достичь оптимальности и эффективности работы робота в различных условиях. Знание и применение этих уравнений способствует разработке более точных и гибких управляющих алгоритмов, что в свою очередь повышает производительность и функциональность робототехнических систем.
Вопрос-ответ

Для чего применяются дифференциальные уравнения в реальной жизни?
Дифференциальные уравнения широко применяются в физике, экономике, биологии, химии и других областях науки, а также в инженерии и технике. Они позволяют описывать и моделировать разнообразные процессы и явления, такие как движение тел, распространение тепла, изменение популяции организмов, рост и распад веществ и многие другие.
Можете привести пример использования дифференциальных уравнений в физике?
Один из примеров использования дифференциальных уравнений в физике - это описание движения материальной точки под действием силы тяжести. Уравнения Ньютона, которые описывают этот процесс, являются дифференциальными уравнениями. Они позволяют определить траекторию движения, скорость и ускорение точки в зависимости от её положения и массы.
Как дифференциальные уравнения применяются в экономике?
В экономике дифференциальные уравнения используются для моделирования динамики рынка товаров и услуг, финансовых рынков и других экономических процессов. Например, они могут помочь предсказать изменение цены на товар, спрос или предложение в зависимости от различных факторов, таких как население, доходы населения, инфляция и т.д.
Какие приложения дифференциальных уравнений существуют в биологии?
Дифференциальные уравнения в биологии применяются для моделирования популяций организмов, распространения болезней, роста и развития живых систем. Например, они могут помочь предсказать динамику изменения численности популяции в зависимости от рождаемости, смертности и взаимодействия среды или моделировать распространение инфекции среди населения.
Можете привести примеры применения дифференциальных уравнений в инженерии?
В инженерии дифференциальные уравнения используются для моделирования и анализа различных физических процессов, таких как распространение звука, электромагнитные поля, теплопередача, колебания и многие другие. Например, они могут помочь в определении распределения температуры в материале при проведении нагревательных процессов или предсказать колебания конструкций в зависимости от внешних сил.



