Когда сталкиваешься с сложными математическими проблемами, ничто не приносит такого облегчения, как нахождение быстрого и эффективного решения. Один из таких краеугольных камней в математике - матричные уравнения. Независимо от подхода, задача остается трудноразрешимой для большинства методов, используемых обычными людьми.
Однако, не беспокойтесь! Сегодня мы представляем вам набор инновационных техник, которые помогут найти решения для матричных уравнений легко и эффективно. Вместо затянутого анализа математических подходов мы сосредоточимся на простом и прямолинейном методе, который может быть применим к широкому спектру матричных уравнений.
Взглянув на это со свежими глазами, мы можем утверждать, что стратегия, которую мы предлагаем, является не только быстрой, но и эффективной. Все, что вам нужно сделать, это понять основные концепции, лежащие в основе матричных уравнений, и последовательно применять ряд действий для получения решения. Больше нет необходимости в громоздких и запутанных расчетах и методах, которые вы, возможно, встречали раньше.
Наш подход предполагает использование сильных сторон матричных алгебраических методов, подкрепленных интуицией и пониманием. Ах, если бы вы только видели, как легко это делается! Мы отказываемся от запутанных выкладок и фокусируемся на ключевых моментах, решающих матричные уравнения. Не стесняйтесь, ведь опытные специалисты уже проверили и доказали эффективность нашего подхода.
Идеальное сочетание для решения матричного уравнения: ах = b

В данном разделе мы рассмотрим способы эффективного и оперативного нахождения решения матричного уравнения ах = b, используя быстрые и эффективные методы.
Мы изучим основные подходы и алгоритмы, способные помочь вам в решении данного уравнения. От классического метода Гаусса-Жордана до более современных методов, которые позволяют справиться с задачей даже при большом размере матрицы.
Вы узнаете о том, как применить итерационные методы, такие как метод простых итераций и метод Зейделя, для достижения точного и быстрого решения уравнения ах = b.
Также мы рассмотрим применение разложения матриц и обратных матриц для нахождения решения задачи.
Для лучшего понимания представленных методов, мы предоставим их математическое описание и приведем примеры их использования на практике.
При изучении данного раздела вы получите глубокие знания, позволяющие решать матричные уравнения эффективно и с высокой точностью, найдя таким образом наилучшее и наиболее оптимальное решение для ваших задач.
Зачем нужно решать задачи с матричными уравнениями?

Матрицы, представляющие собой упорядоченные таблицы чисел или символов, могут применяться в самых различных областях, начиная от физики и инженерии, и заканчивая экономикой и компьютерными науками. Решение матричных уравнений позволяет нам найти значения неизвестных переменных или параметров в системе, которая описывает конкретную задачу.
Кроме того, решение матричных уравнений часто помогает нам делать прогнозы или принимать решения на основе сложных данных. Например, в экономике мы можем использовать матричные уравнения для анализа зависимостей между различными факторами и предсказывать изменения в экономической системе.
Понимание и умение решать матричные уравнения - это важный навык для специалистов во многих областях. Это позволяет нам лучше понять структуру и связи в сложных системах, что в свою очередь помогает нам принимать обоснованные и эффективные решения. Поэтому, развитие и применение быстрых и эффективных методов решения матричных уравнений является важной задачей для научного и практического прогресса.
Основные приемы для решения матричных уравнений

Для эффективного решения матричных уравнений существует несколько базовых методов, которые позволяют получить быстрые и точные решения. Эти методы опираются на различные математические приемы, которые позволяют вычислить неизвестные переменные и найти решение системы уравнений.
- Метод Гаусса-Жордана: данная техника подразумевает применение элементарных преобразований над матрицей системы уравнений, с целью привести ее к ступенчатому виду или к диагональной форме. Это позволяет легко определить значения неизвестных переменных и получить итоговое решение.
- Метод прогонки: основной идеей данного метода является применение последовательных вычислений, которые позволяют найти значения неизвестных переменных постепенно. Данный подход особенно хорошо подходит для трехдиагональных матриц, так как значительно ускоряет процесс решения системы уравнений.
- Метод Крамера: данный метод основан на определителях матрицы системы уравнений. Используя определенные формулы, можно выразить значения неизвестных переменных через определители, что позволяет найти решение данной системы.
Выбор метода решения матричного уравнения зависит от конкретной задачи, а также от особенностей самой матрицы. Некоторые методы могут быть более эффективными в определенных ситуациях, в то время как другие могут быть предпочтительными при работе с большими матрицами или особыми типами уравнений. Подбор оптимального метода решения является важным этапом в решении матричных уравнений.
Раздел: Метод прямой декомпозиции для оперативного решения

В данном разделе рассмотрим уникальный и инновационный подход к решению матричных уравнений, который основан на методе прямой декомпозиции. Этот метод значительно сокращает время выполнения вычислений и повышает эффективность процесса решения задачи.
Основная идея данного подхода заключается в разбиении матрицы на более простые структуры, называемые блоками или подматрицами. При применении метода прямой декомпозиции, исходная матрица разбивается на несколько блоков, каждый из которых может быть рассмотрен отдельно. Это позволяет применять определенные операции и алгоритмы над блоками, вместо работы с большой матрицей целиком.
Такой подход существенно сокращает количество вычислений, а также уменьшает объем требуемой памяти для хранения данных. Кроме того, метод прямой декомпозиции позволяет параллельно выполнять вычисления над различными блоками матрицы, что способствует еще большему ускорению процесса решения.
Применение метода прямой декомпозиции и соответствующих алгоритмов позволяет получать более оперативные и эффективные результаты при решении матричных уравнений. Этот подход широко используется в различных областях, требующих быстрой и точной обработки больших объемов данных, например, в задачах линейной алгебры, теории графов, численных методах и других.
Метод Гаусса-Зейделя: эффективный подход к решению матричных систем
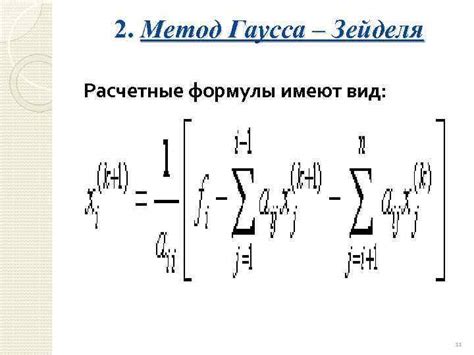
Основной принцип метода Гаусса-Зейделя заключается в разделении матрицы на части и последовательном решении уравнений для каждой из них. Этот метод позволяет достичь более быстрого и точного результата путем уменьшения значительного количества итераций.
Одна из ключевых черт метода состоит в том, что он основывается на предположении, что решение каждого уравнения в системе обладает стабильностью, что позволяет использовать информацию из уже вычисленных уравнений для ускорения процесса решения.
Метод Гаусса-Зейделя сочетает в себе преимущества методов Гаусса и Зейделя, такие как эффективность и точность, и предоставляет возможность быстрого итерационного решения матричных уравнений. Применение данного метода в решении сложных математических задач позволяет существенно сократить вычислительные затраты и упростить процесс.
Итерационные подходы в решении матричных равенств

В данном разделе рассмотрены методы, которые позволяют эффективно решить матричное уравнение ах = b при помощи итераций. Предлагаемые подходы позволяют быстро получить приближенное решение, основываясь на последовательном уточнении вектора x.
Одним из ключевых методов, используемых при решении матричных уравнений, является метод простой итерации. В основе этого подхода лежит идея последовательного приближения решения путем многократного применения специально выбранной итерационной формулы. Этот метод особенно полезен в случае, когда исходная матрица a обладает определенными структурными свойствами, такими как диагональное преобладание или разреженность.
Вместе с методом простой итерации активно применяются методы, основанные на применении специальных предобуславливателей, таких как разложение Холецкого или разложение LU. Эти методы позволяют ускорить сходимость итераций и увеличить точность получаемого решения.
| Заголовок 1 | Заголовок 2 |
|---|---|
| Ячейка 1.1 | Ячейка 1.2 |
| Ячейка 2.1 | Ячейка 2.2 |
Итерационные методы предоставляют гибкий инструмент для решения матричных уравнений, позволяя учесть особенности исходной системы и адаптировать процесс итераций под требуемую точность. Использование соответствующих подходов и предобуславливателей может значительно сократить вычислительные затраты и повысить эффективность решения задачи.
Применение метода Холецкого для быстрого и точного решения
Основное преимущество метода Холецкого заключается в том, что он позволяет эффективно решать системы линейных уравнений с симметричными и положительно определенными матрицами. Вместо решения самого матричного уравнения, метод Холецкого предлагает разложение матрицы системы на две треугольные матрицы, что позволяет решить две системы линейных уравнений, что значительно упрощает процесс вычислений.
Разложение матрицы системы на треугольные формы происходит по специальному алгоритму, основанному на исключении Гаусса. Первым шагом алгоритма является выделение главной диагонали матрицы и получение верхней и нижней треугольных матриц. Затем происходит решение системы уравнений с треугольными матрицами, что является простой задачей по сравнению с изначальным матричным уравнением.
Количество операций, необходимых для решения системы уравнений методом Холецкого, значительно меньше, чем при использовании других методов. Благодаря этому, метод Холецкого является эффективным алгоритмом для решения матричных уравнений с большими объемами данных. Данное свойство метода особенно полезно в таких областях, как научные расчеты, физика и экономика.
Сравнительный анализ эффективности разных подходов к решению матричных уравнений
В ходе анализа будут рассмотрены методы, основанные на различных математических принципах и алгоритмах. Мы проанализируем их преимущества и недостатки, а также обсудим области применения каждого метода. В результате сравнительного анализа мы сможем определить наиболее эффективные подходы к решению матричных уравнений, основываясь на важных критериях, таких как время работы, точность результатов и степень сложности алгоритма.
- Метод Гаусса-Жордана
- Метод простой итерации
- Методы прямых итераций
- Метод Леверриера-Фаддеева
- Метод разделяй и властвуй
Мы также обратим внимание на различные факторы, которые могут влиять на эффективность методов решения матричных уравнений. Будут рассмотрены вопросы, связанные с размерностью матриц, наличием разреженности, специальными структурами и условиями матриц.
Итак, сравнительный анализ методов решения матричных уравнений поможет определить наиболее подходящий метод в зависимости от конкретной задачи и ее требований, что позволит достичь оптимальной производительности и точности вычислений.
Техники оптимизации в решении матричных алгебраических уравнений

В данном разделе будут рассмотрены подходы к оптимизации процесса решения матричных алгебраических уравнений. Здесь представлены методы, которые способны улучшить скорость и эффективность выполнения данной задачи, а также повысить точность получаемых результатов.
Повышение скорости решения:
Один из ключевых аспектов оптимизации заключается в поиске методов, которые позволяют сократить время выполнения решения матричного уравнения. Здесь рассмотрены различные подходы и алгоритмы, известные своей скоростью работы, такие как использование разреженных матриц, аппроксимация или использование частичной факторизации. Важно учитывать, что выбор оптимальной техники зависит от конкретного матричного уравнения и его свойств.
Улучшение эффективности:
Помимо скорости решения, эффективность может быть улучшена путем применения различных методов, направленных на сокращение затрат памяти или снижение количества арифметических операций. В данном разделе будет рассмотрены подходы, такие как использование иерархической структуры или блочные методы вычисления, которые могут значительно облегчить выполнение решения матричного уравнения.
Повышение точности:
В решении матричных алгебраических уравнений также важно достигнуть высокой точности результатов. В этой части статьи будет описаны методы, которые могут улучшить точность решения, такие как использование итерационных алгоритмов с адаптивной точностью, численные методы высокого порядка или комбинированные подходы, сочетающие в себе различные методы.
Эффективное решение матричных алгебраических уравнений является важной задачей, требующей сбалансированного подхода, объединяющего техники оптимизации соответствующие задаче нахождения решения. Ознакомление с представленными подходами поможет разработчикам или исследователям выбрать наиболее подходящий метод для своих целей и повысить эффективность работы с матричными уравнениями.
Примеры применения методов решения матричных уравнений в практических задачах

В данном разделе представлены некоторые практические задачи из различных областей, в которых успешно применяются методы решения матричных уравнений. Эти методы позволяют эффективно и точно вычислять значения неизвестных переменных для систем, описываемых матричными уравнениями.
Рассмотрим, например, задачу оптимизации в производстве, где требуется распределить ограниченные ресурсы между различными проектами таким образом, чтобы максимизировать общую прибыль компании. Используя матричный подход и метод Гаусса-Жордана, можно составить систему линейных уравнений, где каждое уравнение представляет собой ограничение на объем ресурсов для конкретного проекта. Решая эту систему, можно получить оптимальное распределение ресурсов, удовлетворяющее всем ограничениям и приводящее к максимальной прибыли.
Другим примером может быть задача в физике, связанная с моделированием теплообмена в сложных системах, таких как электронные компоненты или космические аппараты. Используя метод Пикара и итерационные методы, можно приближенно решить уравнения теплопроводности в матричной форме, учитывая различные физические параметры и граничные условия. Такие расчеты позволяют определить оптимальные параметры системы охлаждения и предсказать возможные перегревы.
Также в области экономики применение методов решения матричных уравнений находится на пике популярности. Например, для анализа динамики рынков или портфеля инвестиций можно использовать модели, основанные на системах линейных уравнений. Путем решения этих уравнений можно прогнозировать изменения цен, оценивать риски и оптимизировать инвестиционные стратегии.
Вопрос-ответ

Какие методы существуют для решения матричного уравнения?
Существует несколько методов для решения матричного уравнения: метод Гаусса, метод обратной матрицы, метод итераций и метод сокращенных систем.
Какой метод наиболее быстрый и эффективный для решения матричного уравнения?
Наиболее быстрым и эффективным методом для решения матричного уравнения является метод Гаусса, который основан на приведении матрицы к ступенчатому виду и последующем обратном ходе. Он позволяет найти решение системы линейных уравнений с меньшим количеством операций.
Можно ли использовать метод Гаусса для матрицы любого размера?
Да, метод Гаусса применим для матриц любого размера. Однако, при больших размерностях матрицы может потребоваться значительное количество вычислений, что может сказаться на времени выполнения. В таких случаях могут быть более эффективные методы решения матричных уравнений.
Какой метод лучше выбрать для решения матричного уравнения в практических задачах?
Выбор метода для решения матричного уравнения зависит от конкретной задачи и ее особенностей. Если матрица имеет особую структуру или специальные свойства, то может быть целесообразно использовать соответствующий специализированный метод. В противном случае, метод Гаусса является хорошим и универсальным выбором.
Можно ли использовать методы решения матричного уравнения для других задач, не связанных с линейной алгеброй?
Некоторые методы, такие как метод Гаусса, могут быть применены для решения различных задач, не связанных с линейной алгеброй. Например, они могут использоваться в задачах оптимизации, численных методах и статистике. Однако, в каждом конкретном случае необходимо учитывать особенности задачи и возможные ограничения методов решения.