В геометрии всегда найдутся такие фигуры, которые весьма разнообразны и, казалось бы, изучены до мельчайших деталей. К одной из таких фигур относится треугольник, который уже много веков привлекает внимание математиков и исследователей. Каждый треугольник обладает своими особенностями и свойствами, которые важно уметь анализировать и применять в решении задач.
В данной статье мы рассмотрим одну из таких особенностей - равенство стороны АВ треугольника АВС. Есть множество способов и методов, позволяющих решить данную задачу, но одним из наиболее эффективных является использование геометрических принципов и свойств, а также применение алгебраических методов. Мы рассмотрим все возможные варианты и подробно объясним каждый из них, чтобы вы могли легко и успешно применить их в практических задачах.
Основные понятия и термины, связанные с изучением треугольника АВС

- Сторона треугольника: это отрезок, соединяющий две вершины треугольника. В нашем случае, треугольник АВС имеет стороны АВ, ВС и СА.
- Вершина треугольника: это точка, где пересекаются стороны треугольника. В нашем случае, вершины треугольника АВС обозначаются буквами А, В и С.
- Угол треугольника: это область между двумя сторонами треугольника. В треугольнике АВС можно выделить три угла: угол А, угол В и угол С.
- Высота треугольника: это перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противоположную сторону. Высоты треугольника обозначаются hА, hВ и hС.
- Медиана треугольника: это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Медианы треугольника обозначаются mА, mВ и mС.
- Биссектриса треугольника: это прямая, которая делит угол на два равных угла. Биссектрисы треугольника обозначаются bА, bВ и bС.
Теперь, когда мы знакомы с основными терминами, мы можем перейти к подробному изучению равнобедренных, разносторонних, прямоугольных треугольников и других особенностей треугольника АВС, которые помогут нам найти решение задачи о равенстве стороны АВ и значения х.
Значимость равенства АВ = 8 в контексте треугольника АВС
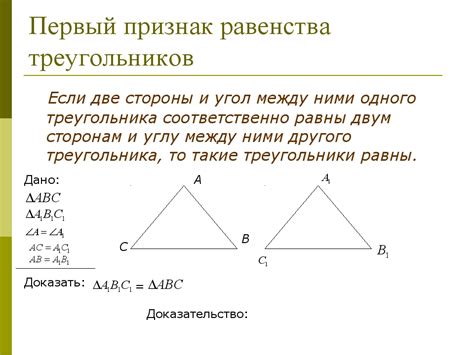
В данном разделе мы рассмотрим важное равенство в геометрии треугольника, которое имеет значение АВ = 8. Оное представляет собой особую особенность, которая влияет на характеристики треугольника и его свойства. Подробно разберем, как это равенство определяет форму и размеры треугольника, а также какие особенности это равенство вносит в его геометрическую структуру.
Сначала приступим к изучению, как данное равенство влияет на длину стороны АВ треугольника АВС. Обратим внимание на то, что значение АВ = 8 указывает на конкретную длину, которая может иметь следствия для других сторон треугольника.
Затем рассмотрим, как равенство АВ = 8 влияет на углы треугольника АВС. Посмотрим, какие возможные значения принимают углы и как они соотносятся друг с другом под влиянием данного равенства.
Далее изучим особенности периметра и площади треугольника АВС, когда значение АВ = 8. Убедимся, как это значение влияет на эти две важные характеристики треугольника и как это связано с размерами его сторон и углами.
Как определить длины сторон треугольника при известной длине одной из сторон
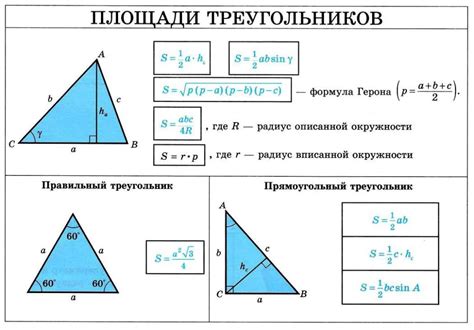
В данном разделе мы рассмотрим методы и алгоритмы для определения длин остальных сторон треугольника, когда известна только длина одной из них.
Наша задача - найти значения сторон треугольника АВС, если известно, что сторона АВ равна 8.
Прежде чем переходить к конкретным методам, стоит упомянуть основную теорему геометрии, которая поможет нам в решении задачи. Она гласит: "В треугольнике, если две стороны равны двух сторонам другого треугольника, а углы между этими сторонами одинаковы, то треугольники равны".
Используя данную теорему, мы можем приступить к поиску длин остальных сторон треугольника АВС. Нам понадобится знание о различных случаях равных треугольников и их свойствах.
Исходя из условия задачи, у нас есть сторона АВ длиной 8. Также, нам известно, что стороны треугольника неотрицательны.
В зависимости от заданного треугольника и его особенностей, мы рассмотрим алгоритмы вычисления значений остальных сторон, такие как: применение тригонометрических функций, использование формулы Пифагора, применение законов косинусов и синусов. Каждый метод имеет свои особенности и может быть применим в определенных случаях.
- Метод 1: Применение тригонометрических функций для определения длины сторон треугольника.
- Метод 2: Использование формулы Пифагора для нахождения длин сторон.
- Метод 3: Применение законов косинусов и синусов для вычисления значений сторон треугольника.
Исходя из данных методов, мы сможем определить значения сторон треугольника АВС и получить полное представление о его структуре и геометрических параметрах.
Особенности и характеристики равнобедренного треугольника АВС

Одним из главных свойств равнобедренного треугольника является равенство оснований, то есть сторон АВ и СВ. Благодаря этому равенству, многие геометрические свойства и вычисления сокращаются до несложных операций.
Одним из интересных свойств равнобедренного треугольника является равенство углов при основаниях. Так, углы ВАС и ВСА имеют одинаковую величину и называются основными углами равнобедренного треугольника.
Еще одной интересной особенностью равнобедренного треугольника является то, что его медиана, проведенная из вершины треугольника, перпендикулярна к основанию и делит его на две равные части.
| Свойство | Описание |
|---|---|
| Равенство сторон АВ и СВ | Две стороны треугольника равны между собой, что облегчает вычисления. |
| Равенство углов ВАС и ВСА | Углы при основаниях равнобедренного треугольника имеют одинаковую величину. |
| Медиана перпендикулярна основанию | Медиана, проведенная из вершины, делит основание на две равные части. |
Равнобедренные треугольники находят применение в различных областях, в том числе в архитектуре, строительстве и геодезии. Изучение их особенностей и свойств важно для понимания принципов построения и анализа геометрических форм.
Определение типа треугольника АВС при известном значении стороны АВ в 8 единиц
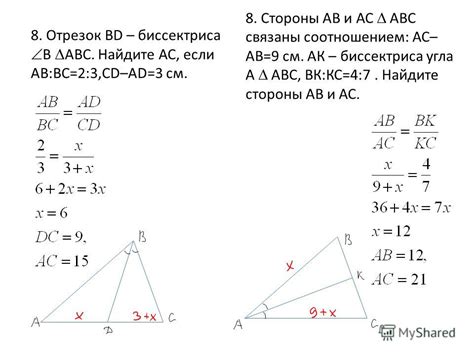
Каждый треугольник уникален и имеет свои особенности. По известному равенству стороны АВ величиной 8 единиц мы можем определить тип треугольника и его свойства.
Существуют различные способы классификации треугольников, и одним из наиболее распространенных является их классификация по длинам сторон. Мы можем определить тип треугольника АВС, используя значение стороны АВ в 8 единиц.
Если все стороны треугольника АВС имеют одинаковую длину, то такой треугольник называется равносторонним. В данном случае, если АВ = 8, и стороны BC и AC также равны 8, то треугольник АВС будет равносторонним.
Если две стороны треугольника имеют одинаковую длину, а третья сторона отличается от них, то такой треугольник называется равнобедренным. Если АВ = 8, а стороны BC и AC имеют разную длину, то треугольник АВС будет равнобедренным.
Если все три стороны треугольника имеют разные длины, то такой треугольник называется разносторонним. В данном случае, если АВ = 8, и стороны BC и AC также отличаются от 8, то треугольник АВС будет разносторонним.
Знание типа треугольника позволяет нам лучше понять его свойства и особенности. В данном случае, зная значение стороны АВ в 8 единиц, мы можем определить тип треугольника АВС и использовать эту информацию в дальнейших расчетах и решении геометрических задач.
Как найти значение стороны АВ, обладающей особыми свойствами

Для начала, обратимся к известным формулам и свойствам, связанным с треугольниками. Важно применить знание о равенстве сторон в треугольнике и применить его к данной задаче.
- Сначала, обратим внимание на существующие равенства сторон в треугольнике АВС.
- Затем, используя синусы треугольника и соответствующие формулы, найдем другие стороны треугольника и углы.
- Далее, учтем особое условие задачи - равенство АВ = 8 - и используем его для нахождения других неизвестных величин.
- И, наконец, применим полученные результаты для нахождения значений остальных сторон и углов треугольника, с учетом данных особых условий.
Таким образом, решив задачу, где необходимо использовать равенство АВ = 8, мы сможем получить значение стороны АВ, которая обладает указанным специальным свойством. Такая задача требует применения знаний и формул, связанных с геометрией треугольников, а также умения логически мыслить и применять полученные сведения для решения конкретных задач.
Роль значения АВ=8 в вычислении различных углов треугольника

В данном разделе мы рассмотрим, как значение стороны АВ, равное 8, оказывает влияние на определение различных углов треугольника. Используя данную информацию, мы сможем получить дополнительные данные о геометрических характеристиках треугольника АВС.
Значение стороны АВ=8 позволяет нам определить отношения между длинами других сторон и углами треугольника. Это также открывает возможность вычислить значения углов треугольника, используя теоремы и свойства геометрии.
- С учетом значения АВ=8, мы можем вычислить длины других сторон треугольника, используя теорему Пифагора или свойства подобных треугольников.
- Зная значения стороны АВ и других сторон треугольника, мы можем определить углы треугольника, используя тригонометрические функции. Например, мы можем использовать теорему косинусов для вычисления углов, если известны длины сторон треугольника.
- Также, имея значение стороны АВ=8, мы можем определить углы треугольника, используя свойства равнобедренных треугольников или прямоугольных треугольников.
- Углы треугольника могут быть также найдены с использованием связи между углами и сторонами треугольника, такой как теорема синусов или теорема косинусов.
Таким образом, значение АВ=8 имеет важное значение при решении геометрических задач. Оно позволяет нам определить дополнительные характеристики треугольника, такие как углы, и использовать различные геометрические теоремы и свойства для вычисления этих углов.
Влияние длины отрезка АВ в заданном значении на площадь данного треугольника

Равенство длины отрезка АВ к значению 8 находит отражение в формуле для расчета площади треугольника АВС. Изучение этого влияния позволяет понять, как изменяется площадь треугольника при изменении длины основания АВ, и какие закономерности можно выявить.
Длина отрезка АВ, равная 8, имеет свое влияние на площадь треугольника. Это позволяет нам классифицировать треугольник и определить его особенности и свойства. Рассмотрение данного равенства приводит к интересным результатам, которые мы рассмотрим в следующих разделах.
Исследование влияния значения 8 на площадь треугольника АВС позволяет нам лучше понять эту геометрическую фигуру и определить отношение между длиной основания и площадью треугольника. Познакомившись с результатами и анализом, вы сможете узнать об интересных особенностях данного треугольника и применить полученные знания в дальнейших задачах и решениях.
Задачи на самостоятельное решение с использованием равенства AV = 8
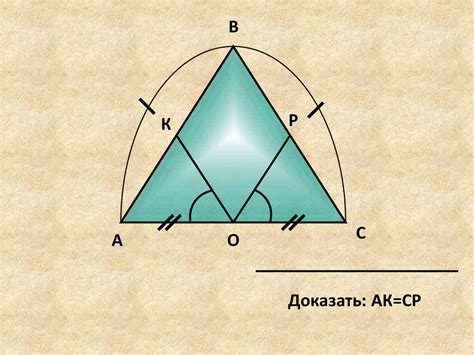
В процессе решения задач необходимо учитывать, что равенство AV = 8 является ключевым моментом. Задачи могут включать построение дополнительных отрезков, нахождение углов или других параметров треугольника. Важно уметь правильно интерпретировать равенство и применять его для решения задач.
Треугольник – геометрическая фигура, состоящая из трех отрезков, соединяющих три точки в плоскости. Если известно, что один из отрезков – AB – равен 8, то это предоставляет возможность решить ряд задач, связанных с данным треугольником.
Основной фокус в задачах данного раздела – использование равенства AV = 8 для нахождения других параметров треугольника. Это может быть нахождение длины других отрезков, вычисление углов, определение типа треугольника или построение дополнительных отрезков. Каждая задача представляет свою уникальную ситуацию, требующую применения знаний и исследования треугольника.
Практическое применение равенства АВ = 8 в геометрии и вычислительной математике
Равенство АВ = 8 в геометрии и вычислительной математике открывает перед нами целый ряд возможностей и приложений. Необходимо отметить, что данное равенство может быть использовано для изучения различных свойств и закономерностей треугольников и других геометрических фигур, а также в решении задач из области вычислительной математики.
Одним из практических применений равенства АВ = 8 является определение длины или площади других сторон и фигур, связанных с треугольником АВС. Например, зная длину стороны АВ и решив задачу с использованием геометрических принципов, мы можем вычислить длину другой стороны треугольника или площадь окружности, вписанной в этот треугольник.
Кроме того, равенство АВ = 8 может быть использовано для проведения различных исследований и экспериментов в области вычислительной математики. Например, мы можем использовать данное равенство для создания компьютерных моделей треугольников и исследования их свойств при изменении других параметров, таких как углы или длины других сторон.
Таким образом, использование равенства АВ = 8 позволяет нам более глубоко понять и исследовать геометрические объекты и применить полученные знания в вычислительной математике. Это открывает перед нами новые возможности и перспективы в развитии этих наук и их применении в практике.
Вопрос-ответ

Какое решение может быть, если длина стороны треугольника АВ равна 8?
Если длина стороны треугольника АВ равна 8, то это означает, что заданная сторона имеет фиксированную величину и не может изменяться. В таком случае, нам остаётся найти остальные стороны и углы треугольника посредством применения различных геометрических методов и формул.
Какие особенности имеет треугольник АВС, если сторона АВ равна 8?
Если длина стороны треугольника АВ равна 8, то это имеет важное значение для этого треугольника. Равенство сторон АВ говорит нам о том, что треугольник АВС является равнобедренным - у него две равные стороны АВ. Это свойство позволяет использовать специальные формулы и методы для нахождения других сторон и углов данного треугольника.
Какие существуют методы нахождения сторон и углов треугольника АВС, если сторона АВ равна 8?
Есть несколько методов, которые позволяют найти стороны и углы треугольника АВС при равенстве длины стороны АВ. Один из них - использование теоремы косинусов, которая позволяет вычислить недостающие стороны и углы треугольника на основе известной стороны и ещё двух сторон или углов. Ещё одним методом является использование свойств равнобедренного треугольника, которые позволяют найти остальные стороны и углы посредством применения изученных формул и связей.
Как можно решить треугольник АВС, если известно, что длина стороны АВ равна 8?
Чтобы решить треугольник АВС при известной длине стороны АВ равной 8, можно использовать различные методы геометрии. Например, можно применить теорему косинусов, которая позволяет вычислить недостающие стороны и углы треугольника по известным данным. Также можно использовать свойства равнобедренного треугольника, чтобы найти остальные стороны и углы. Возможны и другие методы, в зависимости от конкретных условий и задачи.