В мире цифр, графиков и диаграмм среднее значение – это синоним статистической информации, которая помогает понять и оценить различные явления. Этот показатель становится надежным и объективным ориентиром во множестве сфер, от экономики и медицины до социологии и психологии.
Определить и применить среднее значение – значит познать суть и необычность представленных данных, невзирая на их тип или разнообразие. Нельзя недооценивать силу этого показателя, ведь его роль в анализе стремится внедрить справедливость и объективность в объективный мир цифр. В то же время, статистическое определение среднего значения не может быть ограничено одним подходом.
Эмпирические и математические методы используются в одинаковой мере для расчёта средних показателей. Точное и необходимое решение в каждом отдельном случае зависит от специфики данных и задач анализа. Среднее значение – это часть большого пазла, который помогает детализировать и преобразить статистические составляющие, отражая порядок и правдоподобие вокруг нас.
Сущность и важность средней величины в анализе данных

Средняя величина представляет собой мощный инструмент для изучения различных явлений и является основой для дальнейшего анализа данных. Она помогает исследователям получить общее представление о распределении данных и выявить общие тенденции или закономерности.
Кроме того, средняя величина может использоваться для сравнения различных наборов данных и определения их относительной центральной тенденции. Этот показатель также часто используется для сравнения результатов и идентификации аномальных значений.
| Причины использования средней величины: | Результаты использования средней величины: |
|---|---|
| 1. Обобщение исходных данных. | 1. Предоставление общей картины данных. |
| 2. Сравнение различных наборов данных. | 2. Определение относительной центральной тенденции. |
| 3. Идентификация аномальных значений. | 3. Выявление возможных выбросов. |
Важно отметить, что средняя величина может быть подвержена искажениям, особенно в случае наличия выбросов или неравномерности распределения данных. Поэтому для полной оценки набора данных и получения более точных результатов часто требуется использование дополнительных статистических мер, таких как медиана или мода.
Математическое определение среднего значения

Среднее значение позволяет нам получить общую характеристику данных, исключая случайные отклонения и выбросы. Оно основывается на расчете суммы всех значений в наборе данных и их делении на количество этих значений. Таким образом, мы получаем числовую величину, которая выражает центральную тенденцию данных.
Каждый из методов определения среднего значения имеет свои особенности. Например, среднее арифметическое является наиболее распространенным методом и просто вычисляется путем деления суммы всех значений на их количество. Среднее геометрическое, в свою очередь, использует произведение значений и извлекает из них корень степени, равной количеству значений. Это позволяет учесть важность каждого значения в наборе.
Вычисление среднего значения для переменных с непрерывным характером
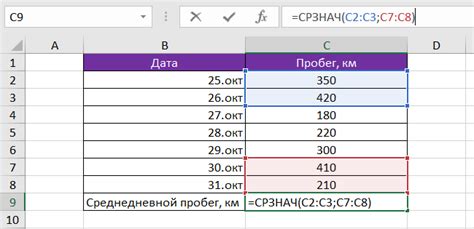
Один из наиболее распространенных способов вычисления среднего значения для непрерывных переменных - это использование формулы для выборочного среднего. Данная формула позволяет нам найти среднее арифметическое для числовых значений, не прерывая их последовательность.
Другим способом вычисления среднего значения для непрерывных переменных является метод группирования данных. Данный метод предполагает разделение значений переменных на интервалы и нахождение среднего значения для каждого из интервалов. Это позволяет упростить анализ данных, особенно при наличии большого объема информации.
Очень важно учитывать особенности распределения непрерывных переменных при вычислении среднего значения. Например, в случае нормального распределения мы можем использовать формулу для расчета среднего арифметического, однако в случае скошенного распределения может потребоваться применение других методов, например, медианы или моды.
| Метод | Описание | Применение |
|---|---|---|
| Формула выборочного среднего | Вычисление среднего арифметического для числовых значений | Общая мера центральной тенденции |
| Метод группирования данных | Разделение значений переменных на интервалы и вычисление среднего для каждого интервала | Упрощение анализа больших объемов информации |
Расчет среднего значения для дискретных переменных

Для анализа данных, представленных в дискретной форме, необходимо осуществить вычисление среднего значения. Этот показатель позволяет получить представление о типичном значении переменной в выборке. В данном разделе мы рассмотрим методы и алгоритмы расчета среднего значения для дискретных переменных.
Одним из способов вычисления среднего значения является использование формулы, основанной на суммировании всех значений переменной и делении их на количество наблюдений. Другим методом является использование частотной таблицы, в которой переменная разбивается на категории и указывается количество наблюдений в каждой категории. После этого производится умножение каждого значения на его частоту, а затем все значения складываются и делятся на общее количество наблюдений.
При вычислении среднего значения для дискретных переменных также может использоваться взвешенное среднее значение, которое учитывает разные веса значений переменной. В этом случае, каждому значению переменной присваивается определенный коэффициент веса, который учитывает его важность в анализе данных.
- Метод суммирования значений и деления на количество наблюдений.
- Использование частотной таблицы для расчета среднего значения.
- Расчет взвешенного среднего значения.
Таким образом, выбор метода вычисления среднего значения для дискретных переменных зависит от особенностей данных и целей исследования. Знание этих методов позволяет провести анализ данных эффективно и получить более точные результаты.
Основные характеристики среднего арифметического и его особенности

Когда мы говорим о среднем арифметическом, мы имеем в виду значение, которое получается путем сложения всех чисел в наборе данных и деления суммы на количество этих чисел. Это метод позволяет получить числовую оценку центральной тенденции, или типичного значения в наборе данных. Среднее арифметическое может быть полезно при анализе, так как оно позволяет суммировать и упрощать информацию, выявлять основные тенденции и сравнивать результаты.
- Преимущества среднего арифметического:
- Объективность: среднее арифметическое позволяет получить четкую и конкретную цифровую оценку значения набора данных.
- Простота: расчет среднего арифметического может быть осуществлен без необходимости в специальных знаниях или сложных формул.
- Универсальность: концепция среднего арифметического может быть применена к различным типам данных, включая числовые значения, проценты или даже ранги.
Однако использование среднего арифметического также имеет некоторые особенности и ограничения. Известно, что среднее арифметическое чувствительно к выбросам в данных, так как оно зависит от каждого элемента в наборе. Если в наборе имеется одно или несколько значений, которые значительно отличаются от остальных, это может исказить результат и привести к неправильной оценке. Кроме того, среднее арифметическое может не учитывать распределение данных и не давать полного представления о вариативности и разнообразии в наборе.
В целом, среднее арифметическое является важным инструментом статистики, который может помочь в анализе данных и принятии информированных решений. Однако при его использовании необходимо учитывать его особенности и применять с осторожностью, чтобы полноценно понять и интерпретировать результаты их значения.
Иные методы вычисления арифметического среднего

В данном разделе представлены альтернативные подходы к определению значений центральной тенденции набора данных. Вместо классического среднего значения и его расчета путем суммирования и деления на количество наблюдений, здесь рассматриваются другие способы оценки центрального значения, позволяющие учесть различные особенности и распределение данных.
Первый метод, который можно использовать, - это медиана. Медиана представляет собой значение, расположенное посередине отсортированного набора данных. Она позволяет избежать влияние выбросов и экстремальных значений на итоговую оценку. Вторым способом является мода – значение, которое наиболее часто встречается в наборе данных. Мода позволяет выявить наиболее типичные значения и определить основные пики распределения.
- Квантили представляют собой другой способ определения центрального значения. Квантили делят набор данных на равные части и описывают, как распределены значения в наборе. Например, перцентили – это квантили, которые разделяют набор данных на 100 равных частей. Этот метод позволяет лучше понять, как данные распределены и какое значение считается «высоким» или «низким».
- Еще одним методом является среднее гармоническое. Оно учитывает различные взаимосвязи и пропорции между отдельными значениями в наборе данных. Среднее гармоническое полезно, когда значения должны быть рассмотрены в контексте друг друга.
- В некоторых случаях полезно использовать взвешенное среднее. Оно дает разным значениям различный вес при расчете среднего значения. Например, при работе с набором данных, где некоторые значения представляют большую значимость или имеют более точные измерения, можно применить взвешенное среднее для более точного отражения центрального значения.
Выбор метода вычисления среднего значения зависит от природы данных и цели исследования. Важно учитывать специфику данных и выбирать подход, который наилучшим образом отображает центральную тенденцию набора данных, а также учитывает особенности распределения.
Роль среднего значения в анализе статистической информации

Среднее значение - это показатель, который используется для описания центральной тенденции в наборе данных. Оно представляет собой среднюю величину или уровень, который можно рассматривать как представительный для всей выборки.
- При анализе экономических показателей среднее значение помогает понять общую тенденцию и установить, насколько она отличается от среднего значения в других регионах или периодах.
- В медицинских исследованиях среднее значение может использоваться для определения эффективности лечения или выявления изменений в состоянии здоровья пациента.
- В образовательной статистике среднее значение может указывать на уровень успеваемости школьников или эффективность преподавательской деятельности.
Помимо применения для описания центральной тенденции, среднее значение также является основой для расчета других статистических показателей, таких как дисперсия и стандартное отклонение, которые помогают оценить изменчивость данных.
Таким образом, среднее значение играет важную роль в статистическом анализе, позволяя исследователям обобщать информацию, выявлять закономерности и принимать обоснованные решения на основе доступных данных.
Ограничения и сложности применения арифметического среднего

Одной из проблем применения среднего значения является влияние выбросов - экстремальных значений, которые значительно отличаются от остальных данных. Такие выбросы могут серьезно исказить значение среднего и сделать его неинтерпретируемым. Для обнаружения и учета выбросов необходимо проводить соответствующие статистические анализы и применять методы обработки данных.
Другая проблема, связанная с использованием среднего значения, – это возможность искажения результатов из-за неравномерного распределения данных. При неравномерном распределении среднее значение может не отражать характеристику основной массы данных, а быть сдвинутым в сторону экстремальных значений. В таких случаях предпочтительнее использовать медиану - показатель, который равен значению, расположенному посередине упорядоченного ряда данных.
Еще одной сложностью применения среднего значения является его чувствительность к выборочным изменениям в данных. Даже небольшие изменения в значениях могут привести к существенным изменениям в среднем значении. Поэтому необходимо проводить анализ выборки и оценивать стабильность и надежность полученных результатов.
И наконец, важно учитывать, что арифметическое среднее не всегда является наиболее информативным показателем, особенно в случаях, когда данные имеют разные единицы измерения или неоднородную природу. В таких ситуациях предпочтительнее использовать другие показатели, которые учитывают специфику данных и обеспечивают более полное представление об их характеристиках.
Значимость среднего показателя при принятии решений
Ключевая роль среднего значения:
Среднее значение позволяет суммировать информацию из всего набора данных и предоставляет некий образовательный сигнал, который помогает интерпретировать результаты и принимать решения на основе этих данных. Оно является показателем центральной тенденции, который сглаживает выбросы и избыточные наблюдения, учитывая разнообразные аспекты в данных.
Оценка и сравнение путей:
Среднее значение позволяет сравнивать различные группы или образцы. Оно может использоваться для определения влияния определенных факторов на результаты и для выявления паттернов или различий между группами данных. Сравнительный анализ средних значений может помочь выявить связи, тренды или закономерности, что в свою очередь может быть полезно при принятии решений.
Указание на изменения:
Среднее значение дает представление о средней тенденции в данных, и поэтому может служить индикатором изменений. Если среднее значение значительно отличается от ожидаемого, это может сигнализировать о наличии проблем или изменениях, требующих внимания и принятия соответствующих мер. Следовательно, среднее значение является ориентиром для оценки изменений в данных и принятия связанных с ними решений.
Таким образом, среднее значение играет важную и значимую роль в контексте принятия решений, предоставляя информацию о центральной характеристике набора данных и помогая сравнивать группы, выявлять изменения и управлять различными аспектами на основе этих данных.
Вопрос-ответ

Какое значение имеет среднее значение в статистике?
Среднее значение в статистике представляет собой числовую меру, которая показывает средний уровень числового показателя в наборе данных. Оно является одним из основных способов описания и анализа данных.
Как можно найти среднее значение в статистике?
Среднее значение можно найти, сложив все числовые значения в наборе данных и разделив полученную сумму на количество этих значений. Другой способ - умножить каждое значение на его частоту и сложить их, затем разделить на сумму всех частот. Также существуют различные математические формулы для нахождения среднего значения в разных случаях.
Какое значение имеет медиана по сравнению со средним значением?
Медиана и среднее значение являются двумя разными способами измерения центральной тенденции в наборе данных. В отличие от среднего значения, медиана представляет собой числовое значение, которое находится в середине упорядоченного по возрастанию или убыванию ряда чисел. В некоторых случаях медиана может быть более репрезентативной мерой центральной тенденции, особенно если в данных есть выбросы или аномальные значения.
В каких сферах применяется среднее значение в статистике?
Среднее значение широко используется в различных сферах, таких как экономика, финансы, медицина, образование и другие области, где требуется анализ и описание данных. Например, среднее значение может использоваться для расчета средней зарплаты в определенной отрасли, оценки эффективности лекарственного препарата, определения успеваемости учеников и принятия решений на основе данных.
Какое значение может иметь среднее значение в случае искаженных данных или выбросов?
Если данные искажены или содержат аномальные выбросы, среднее значение может быть искажено и не отражать реальную ситуацию. Например, если в наборе данных есть несколько крайне больших или крайне маленьких значений, то среднее значение может быть значительно выше или ниже, чем ожидаемое. В таких случаях рекомендуется использовать дополнительные меры центральной тенденции, такие как медиана или мода, чтобы получить более точное представление о данных.
Зачем нужно находить среднее значение в статистике?
Среднее значение в статистике используется для оценки центральной тенденции данных, когда нужно получить представление о типичном значении в выборке.



