Когда мы обнаруживаем наше внимание притянутым к миру геометрии, мы начинаем разгадывать необычные загадки, с помощью которых она тайно общается с нами. Одна из таких загадок включает в себя размышления о возможности существования третьей прямой, которая пересечет две уже известные прямые. Вопрос настолько интригующий, что мы, запутавшись в неделимых связях геометрических форм, стремимся открыть ответы, скрывающиеся за множеством удивительных возможностей.
Приключение, которое открывается перед нами, непременно вызывает трепет. Мы ловим себя на мысли, что границы пространства могут быть преодолены, и третья прямая может явиться к нам на помощь. Но, если говорить о геометрии, все не так просто, как может показаться на первый взгляд.
В глубинах геометрии скрываются сокровища, и, преследуя их, мы вступаем в битву с абстрактными понятиями и недосягаемыми идеями. Это как путешествие по лабиринту форм и размеров, где мы даем все силы, чтобы пройти этот путь размышлений и открыть ответ на главный вопрос: существует ли третья прямая, способная пересечь две уже известные?
Определение третьей линии
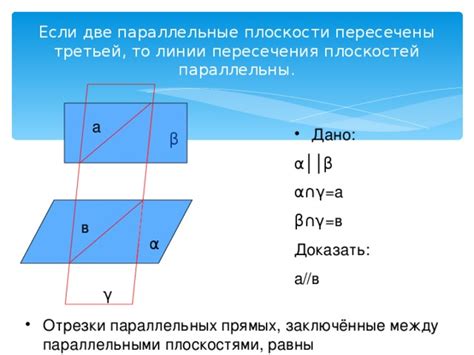
В геометрии существует интересная задача о поиске третьей прямой, которая пересекает две другие линии. Эта загадочная прямая, несомненно, вызывает интерес и требует внимательного рассмотрения.
Обратимся к определению. Третья прямая - это линия, которая проходит сквозь две другие линии, пересекая их в определенной точке. Она является дополнением к уже существующим линиям, создавая геометрическую систему с новыми свойствами и особенностями.
Третья прямая может иметь различный угол наклона относительно других линий и может пересекать их как под прямым углом, так и под различными углами. Это зависит от положения точки пересечения и характеристик уже существующих линий.
Изучение третьей прямой позволяет глубже понять геометрические законы и правила, расширить способы решения задач и увидеть новые возможности в геометрическом пространстве.
Почему искать дополнительную прямую важно?

Зачастую в геометрии нам требуется решить различные задачи, связанные с взаимным расположением прямых. Иногда, для полного понимания или решения задачи, нам необходимо найти третью прямую. Поиск этой дополнительной линии позволяет нам получить дополнительную информацию о взаимодействии между уже имеющимися прямыми.
Нахождение третьей прямой может помочь нам определить области пересечения, параллельность или пересечение линий. Это может быть полезно при решении задач о планировании трасс, определении наиболее эффективного маршрута или рассмотрении схем расположения объектов.
Решение геометрических задач с помощью поиска дополнительной прямой позволяет нам развивать навыки логического мышления и абстрактного мышления. Также это помогает нам понять основные концепции геометрии и улучшить наше понимание пространственных отношений.
| Смысл | Значение |
| Важность | Существенность |
| Полезность | Выгодность |
| Определение | Установление |
Неоднозначные моменты

В рамках данной темы возникают некоторые моменты, требующие дополнительного разъяснения и более глубокого понимания. Некоторые аспекты геометрической задачи, связанной с существованием третьей прямой, которая может пересекать две другие прямые, вызывают определенные трудности и неоднозначность в трактовке. В данном разделе рассмотрим неясные аспекты, представим для них возможные различные точки зрения и попытаемся разобраться в сложной геометрической ситуации.
- Потенциальные сценарии пересечения: Возникает вопрос о возможных вариантах пересечения двух прямых и наличии третьей прямой, удовлетворяющей этому условию. Возможно ли, что прямые пересекаются точкой, либо существует несколько точек пересечения? Или в какой ситуации возможно отсутствие пересечения третьей прямой? Возможные ответы на эти вопросы могут варьироваться в зависимости от подхода к задаче.
- Возможные геометрические условия: Исследуем и анализируем различные геометрические условия, которые необходимо учесть при проведении третьей прямой через две другие. Определим, какие параметры могут влиять на существование и положение третьей прямой. Рассмотрим потенциальные причины неоднозначности и разнообразные виды геометрических заданий, требующих пересечения прямых.
- Разные точки зрения: Представим различные точки зрения и подходы к решению геометрической загадки. Узнаем, какие аргументы может привести каждый подход и какими доводами он обосновывает свое решение. Исследуем возможные сравнительные анализы и альтернативные точки зрения от разных исследователей, математиков и геометров.
- Дополнительные факторы: Рассмотрим также возможные внешние факторы, которые могут влиять на решение этой геометрической задачи. Возможно, некоторые ограничения или условия, не являющиеся очевидными, играют значимую роль в возможности нахождения третьей прямой, пересекающей две другие. Исследуем, как эти факторы могут изменить восприятие и понимание задачи.
Вместе с тем, проводя анализ неоднозначных моментов и вариантов различных сценариев пересечения прямых, мы сможем более полно разобраться в геометрической задаче и обрести глубокое понимание этой загадки.
Когда две прямые пересекаются?

В геометрии мы часто сталкиваемся с вопросом о пересечении двух прямых линий. Ответ на этот вопрос может быть не таким очевидным, как может показаться. Но разберемся вместе! Узнаем, когда и как две прямые могут пересечься и какие условия должны быть выполнены.
Когда две прямые пересекаются, они встречаются в точке, которая называется точкой пересечения. Обычно важно понять, пересекаются ли прямые в одной точке или они могут иметь несколько точек пересечения. Во-первых, для того чтобы прямые пересеклись, они должны быть в одной плоскости - плоскости, где мы рассматриваем эти линии. Во-вторых, прямые не должны быть параллельными, иначе они никогда не пересекутся. Если прямые не являются параллельными и лежат в одной плоскости, их пересечение может быть единственным или может быть бесконечным количеством.
Пересечение двух прямых - это важное понятие в геометрии, оно помогает нам анализировать и изучать различные формы и конструкции. Подробнее разбираясь в условиях и способах пересечения прямых, мы сможем лучше понять основы геометрии и ее приложения в реальном мире. Путем рассмотрения примеров и экспериментов мы сможем углубить наши знания в этом увлекательном предмете.
Возможность пересечения третьей прямой с двумя другими
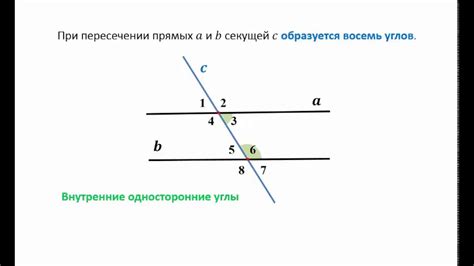
Может ли третья прямая пересечься с двумя другими? Этот вопрос волнует многих любителей геометрии. Ответ на него может иметь как положительный, так и отрицательный характер. Рассмотрим некоторые из возможных сценариев.
| Ситуация | Описание |
|---|---|
| Пересечение в одной точке | Если две прямые пересекаются в точке, то возможно, что третья прямая также проходит через эту точку. Это может быть случай пересечения прямых в плоскости или трехмерном пространстве. |
| Прямые параллельны | Если две прямые параллельны, то третья прямая не может их пересечь. В этом случае, третья прямая может либо лежать в плоскости, образованной параллельными прямыми, либо быть перпендикулярной этой плоскости. |
| Прямые совпадают | Если две прямые совпадают, то третья прямая также будет совпадать с ними. В этом случае, все три прямые будут идти одной линией и пересекаться в каждой точке на этой линии. |
| Прямые скрещиваются | Если две прямые скрещиваются, то третья прямая может пересекать их в разных точках. Расстояние между точками пересечения будет зависеть от угла, под которым прямые скрещиваются. |
Таким образом, существует несколько возможных вариантов взаимодействия третьей прямой с двумя другими. Результат зависит от положения и взаимоотношений между этими прямыми. В дальнейшем, в зависимости от конкретной ситуации, можно применять различные методы и теоремы геометрии для определения возможности пересечения третьей прямой с данными двумя прямыми.
Какие условия нужно выполнить для существования дополнительной прямой, пересекающей две другие?

Для того чтобы определить существование третьей прямой, пересекающей две другие, необходимо учесть геометрические условия. Во-первых, прямые должны лежать в одной плоскости. Это означает, что все три прямые должны быть направлены в одном и том же направлении и не должны быть параллельны друг другу. Во-вторых, точка пересечения двух прямых не должна лежать на третьей прямой. Это гарантирует, что третья прямая будет пересекать обе предыдущие прямые.
Если говорить более формально, условия для существования третьей прямой, пересекающей две другие, можно выразить в следующей форме:
- Прямые должны быть не параллельными.
- Прямые должны лежать в одной плоскости.
- Точка пересечения двух прямых не должна лежать на третьей прямой.
И только если все данные условия выполняются, мы можем говорить о существовании третьей прямой, пересекающей две другие.
Законы геометрии: понимание прямых и их взаимосвязи

В геометрии существуют определенные законы, которые определяют взаимосвязь между прямыми. Одним из таких законов является теорема о пересечении прямых. Эта теорема утверждает, что если две прямые пересекаются, то есть точка, в которой они пересекаются, и эта точка уникальна. Однако, возникает вопрос: существует ли третья прямая, пересекающая две уже существующие?
Ответ на этот вопрос зависит от требований и условий, заданных в задаче или ситуации. В некоторых случаях может существовать третья прямая, пересекающая две другие, в то время как в других случаях такой прямой может не существовать. Понимание геометрических законов и их применение позволяют определить возможность существования третьей прямой и решить геометрическую задачу или загадку.
Изучение геометрии и ее законов помогает развивать абстрактное мышление, улучшает навыки рассуждения и аналитического мышления. Знание геометрических законов позволяет решать сложные проблемы и находить рациональные решения в различных областях науки и техники.
Прямые и плоскости: Взаимодействие линий в трехмерном пространстве
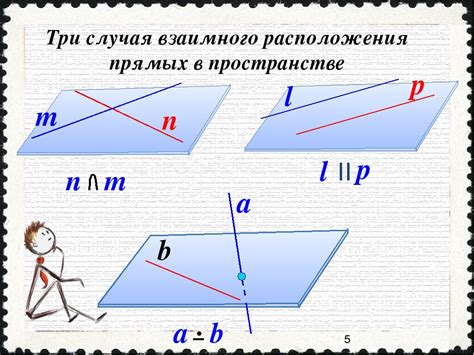
В геометрии широко применяются понятия прямых и плоскостей для описания трехмерных объектов в пространстве. Изучение взаимодействия линий и плоскостей позволяет решать разнообразные задачи и загадки, связанные с геометрией. В данном разделе мы рассмотрим основные принципы и свойства, позволяющие понять, существует ли третья прямая, пересекающая две заданные линии, и какие условия должны быть выполнены для достижения такого пересечения.
Прямые в трехмерном пространстве могут быть лежащими в одной плоскости или параллельными друг другу. Они также могут пересекаться и образовывать точки пересечения, если их направления не совпадают. Для определения существования третьей прямой, пересекающей заданные линии, необходимо анализировать их взаимное расположение и углы между ними.
Для того, чтобы две прямые пересеклись, необходимо, чтобы они лежали в разных плоскостях и имели общую точку пересечения. Если две прямые параллельны друг другу, то третья прямая, пересекающая обе, не существует. Однако, если угол между прямыми не равен 0° или 180°, то существует возможность построить третью прямую, пересекающую их внутри плоскости. Это свойство прямых позволяет решить множество задач, связанных с геометрическими конструкциями.
Исследование свойств и взаимодействия прямых и плоскостей является важной частью геометрии и находит применение в различных областях, включая инженерное проектирование, архитектуру и компьютерную графику. Понимание геометрических законов и правил позволяет анализировать трехмерные объекты и решать сложные задачи в пространстве.
Теорема о наличии дополнительной прямой
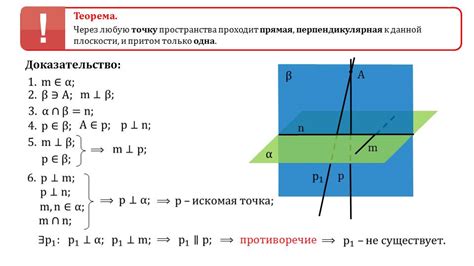
При изучении геометрии мы часто сталкиваемся с вопросом о наличии дополнительной прямой, которая могла бы пересечь две другие. В данном разделе мы рассмотрим функцию такой дополнительной линии и проанализируем условия ее существования.
- Теорема 1: В случае, когда две прямые пересекаются, существует бесконечное множество дополнительных прямых, которые также пересекаются с этими двумя прямыми и создают новые точки пересечения.
- Теорема 2: Если две прямые параллельны, наличие дополнительной прямой, пересекающей обе эти линии, невозможно.
Следовательно, с помощью данных теорем мы можем утверждать, что в случае пересечения двух прямых наличие дополнительной прямой является неотъемлемой частью геометрического пространства. Однако при наличии параллельных прямых, возможность существования такой дополнительной прямой отсутствует.
Вопрос-ответ

Как найти третью прямую, пересекающую две другие?
Для того чтобы найти третью прямую, пересекающую две другие, необходимо определить их положение относительно друг друга. Если две прямые пересекаются, то третья прямая может быть проведена через точку пересечения. Если же прямые параллельны, то третья прямая не сможет их пересечь. Если прямые лежат на одной прямой, то третья прямая может быть проведена по любой из бесконечного числа направлений.
Может ли третья прямая быть параллельна двум другим?
Да, третья прямая может быть параллельна двум другим, если эти две прямые не пересекаются. Если две прямые пересекаются, то третья прямая не может быть параллельна им обоим. В геометрии, параллельные прямые не пересекаются и лежат в одной плоскости.
Есть ли варианты, когда третья прямая не может быть проведена?
Да, есть несколько вариантов, когда третья прямая не может быть проведена. Например, если две прямые лежат на одной прямой, то третья прямая тоже будет лежать на этой прямой, и ее нельзя будет провести в другом направлении. Также, если две прямые параллельны, то третья прямая не сможет их пересечь и также не будет проведена.
Может ли третья прямая иметь бесконечное количество точек пересечения с двумя другими прямыми?
Нет, третья прямая не может иметь бесконечное количество точек пересечения с двумя другими прямыми. Если две прямые пересекаются, то существует только одна точка пересечения, через которую можно провести третью прямую. Если прямые параллельны, то они никогда не пересекаются, и следовательно, третья прямая не сможет иметь точек пересечения с ними.