Очень часто мы рассматриваем натуральные числа как отдельную категорию в математике. Они являются основой нашего счета и позволяют нам измерять и описывать мир вокруг нас. Но что если я скажу вам, что даже в этой простой и понятной области могут существовать необычные исключения?
Именно здесь начинается интересный и удивительный мир математики, где обычные правила иногда нарушаются. Мы знакомы с понятием целых чисел, которые включают в себя все положительные и отрицательные числа, а также ноль. Но что если я скажу вам, что есть такие натуральные числа, которые не являются целыми по определению?
В таком случае возникает вопрос: какие именно числа являются исключением? И как это связано с определением натуральных чисел? Давайте рассмотрим эту тему более подробно и обнаружим, что даже в научных и математических областях существуют загадочные исключения.
Различия между натуральными числами и целыми числами
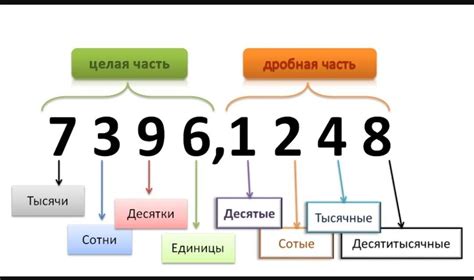
Итак, давайте разберемся, в чем заключаются основные различия между натуральными числами и целыми числами.
Начнем с того, что оба этих понятия относятся к числовым системам и играют важную роль в математике. Но в то время как натуральные числа представляют собой положительные числа, которые используются для подсчета объектов или измерения количества, целые числа включают в себя не только положительные числа, но и отрицательные числа, а также ноль.
Натуральные числа часто используются в повседневной жизни для перечисления предметов или учета количества. Они обозначаются символом N и могут быть представлены последовательностью: 1, 2, 3, 4, 5 и так далее.
Однако целые числа, помимо положительных натуральных чисел, также включают все отрицательные числа, которые используются для указания долгов или дефицита, и ноль, который указывает отсутствие объекта или нулевое количество.
| Натуральные числа | Целые числа |
|---|---|
| 1, 2, 3, 4, 5... | ..., -3, -2, -1, 0, 1, 2, 3... |
Таким образом, целые числа являются расширением натуральных чисел, включая положительные, отрицательные числа и ноль, и предоставляют возможность учета не только количества предметов, но и других аспектов, таких как отрицательные значения и нулевое количество.
Основные свойства натуральных чисел и целых чисел.
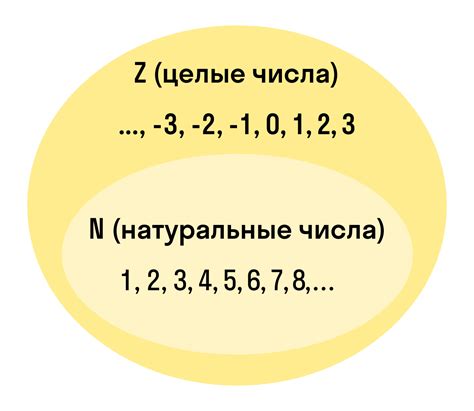
Значительным отличием целых чисел от натуральных является возможность представлять отрицательные числа. Основной чертой целых чисел является наличие нуля, который является нейтральным элементом в математических операциях. Целые числа включают в себя натуральные числа, а также отрицательные числа, которые значат отсутствие определенного количества предметов или состояние долга, тепла и других понятий.
- Натуральные числа являются подмножеством целых чисел.
- Целые числа включают в себя натуральные, отрицательные числа и ноль.
- Натуральные числа упорядочены по возрастанию, начиная с единицы.
- Целые числа могут быть упорядочены на числовой прямой, включая отрицательные значения слева от нуля и положительные значения справа от нуля.
- Сумма, разность и произведение натуральных чисел всегда являются натуральными числами.
- Сумма и разность целых чисел также являются целыми числами.
- Целые числа можно складывать, вычитать и перемножать, тем самым получая новые целые числа.
Понимание основных свойств натуральных и целых чисел является важным при изучении более сложных математических концепций. Эти числа играют важную роль в алгебре, арифметике и других разделах математики, обеспечивая надежную основу для решения различных задач и проблем.
Исключительные случаи, когда натуральные числа не являются целыми
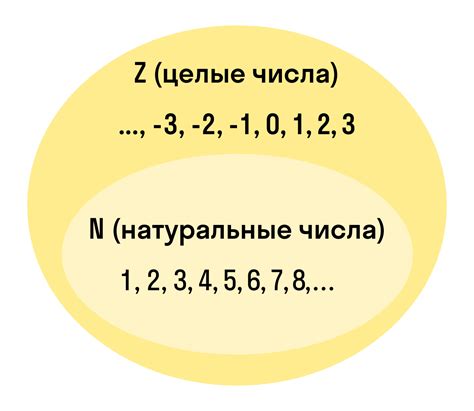
В некоторых особых условиях, существуют ситуации, когда обычно положительные целые числа приобретают некоторые особенности и перестают быть целыми числами. Эти исключительные случаи открывают новые варианты и взгляды на классификацию чисел и их свойства.
Первый исключительный случай
В некоторых математических моделях натуральные числа могут приобретать дробную или периодическую форму записи. Это происходит, когда некоторые факторы или ограничения влияют на их разделение или представление в определенной системе счисления.
Второй исключительный случай
При решении определенных задач или при проведении исследований в некоторых научных областях, натуральные числа могут претерпевать трансформации и становиться комплексными числами. Это позволяет ученным моделировать и описывать более сложные процессы или явления, которые не могут быть полностью представлены только целыми числами.
Таким образом, необходимо учитывать эти особенные случаи, чтобы иметь полное представление о всевозможных формах и свойствах чисел. Это открывает новые возможности для математических и исследовательских исследований, а также помогает лучше понимать сложные системы и процессы, где целые числа не всегда являются их основой.
Понятие нерациональных чисел и их связь с натуральными числами

В математике существует классификация чисел на рациональные и нерациональные. Рациональные числа представляют собой дроби, которые могут быть представлены в виде отношения двух целых чисел. Однако, нерациональные числа не могут быть представлены в такой форме и не могут быть точно выражены как конечная или периодическая десятичная дробь.
Натуральные числа являются одной из основных частей числовой системы и включают в себя числа от 1 до бесконечности. Они применяются для подсчета, нумерации и классификации объектов в реальном мире. Натуральные числа являются целыми и положительными, и они играют важную роль в алгебре и арифметике.
Отношение между натуральными числами и нерациональными числами заключается в том, что натуральные числа являются подмножеством нерациональных чисел. Возможно, это неочевидно, но каждое натуральное число может быть записано в виде нерационального числа путем добавления десятичных нулей после запятой. Например, число 5 можно представить как 5.000000... или 5.000000000... и так далее. Таким образом, все натуральные числа могут быть рассмотрены как нерациональные числа, хотя их специальной классификации как нерациональных чисел обычно не производится.
Таким образом, общая идея заключается в том, что натуральные числа, как часть числовой системы, имеют отношение к нерациональным числам, но они не считаются нерациональными числами в строгом смысле. Вместо этого, натуральные числа представляют собой особую категорию в числовом спектре, играющую важную роль в различных областях математики и ее применении.
Примеры натуральных чисел, не обладающих целым значением
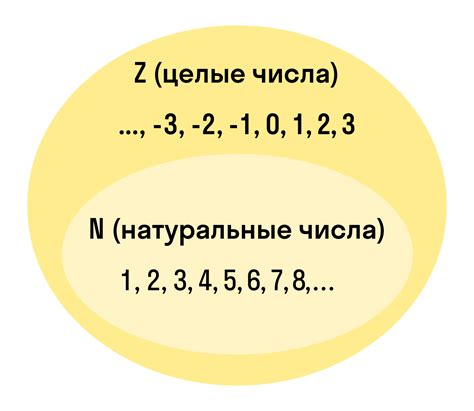
В числовой системе широко распространены числа, которые можно представить в виде целой части и дробной части. Однако существуют некоторые натуральные числа, к которым нельзя применить данное представление. Эти числа не могут быть разделены на целую и дробную части, так как они не обладают целым значением.
Один из примеров таких чисел - число "пи" (π). Это иррациональное число, которое является бесконечной десятичной дробью. Значение числа "пи" равно приблизительно 3.141592653589793238... и не может быть точно представлено в виде целого числа.
Другим примером является число "экспонента" (е). Это также иррациональное число и является основанием натурального логарифма. Значение числа "экспонента" равно приблизительно 2.718281828459045235... и не может быть выражено в виде простого целого числа.
Также существуют трансцендентные числа, которые являются особым классом чисел и не обладают свойством быть целыми. Одним из известных примеров является число "е", упомянутое ранее, а также число "пи" и некоторые другие.
Таким образом, примеры натуральных чисел, не обладающих целым значением, включают в себя иррациональные числа и трансцендентные числа. Эти числа представляют особый интерес в математике и имеют важное значение в различных научных и практических областях.
Возможные объяснения и причины возникновения особых случаев

1. Особенности арифметических операций Некоторые математические операции, такие как деление и извлечение корня, могут привести к появлению дробных значений, даже когда исходные данные являются натуральными числами. Это связано с особенностями в вычислительных методах и точности представления чисел в компьютерных системах. |
2. Влияние окружающей среды Часто в реальном мире существуют условия, которые могут приводить к появлению исключительных ситуаций. Например, при измерении некоторых физических величин могут возникнуть факторы, которые не позволяют получить целочисленное значение. Это может быть обусловлено как внешними воздействиями, так и допущенными ошибками в процессе измерения. |
3. Математические модели и концепции В некоторых областях математики и науки существуют специфические модели и концепции, в которых допускается использование нецелых значений для описания явлений. Это может быть связано с временным характером, вероятностными расчетами или абстрактными представлениями. В таких моделях целочисленность может быть нарушена в силу специфических требований и логики их использования. |
Важность понимания искючительных ситуаций в различных сферах научных исследований

Глубокое понимание и учет исключительных ситуаций имеет огромное значение для различных областей научных исследований. В рамках таких сфер как физика, химия, биология, психология и экономика, способность обнаружить и объяснить редкие, непредсказуемые и отклоняющиеся от общего закона явления, может привести к значительным прорывам.
Исключительные случаи могут являться ключом к пониманию глубинных законов природы и могут привнести новые понятия и концепции в наше понимание мира. Например, наблюдение необычного поведения элементарных частиц в физике высоких энергий может указывать на существование новых физических моделей или открывать возможность новых технологических решений.
В области биологии, учет исключительных ситуаций может приводить к открытию новых видов, пониманию процессов эволюции и развития живых организмов. Непредсказуемые результаты экспериментов часто выявляют фундаментальные закономерности, которые ранее не были известны.
Более того, в экономике и финансовой сфере учет и понимание исключительных случаев может помочь в принятии важных решений, спрогнозировать риски и предотвратить финансовые кризисы. Анализ таких случаев может привести к открытию новых рыночных возможностей, стратегий и технологий.
Таким образом, искючительные ситуации играют важную роль в науке, открывая новые горизонты для исследователей и помогая в дальнейшем развитии различных областей знания. Глубокое понимание и учет исключительных случаев приводит к прорывам в наших теоретических концепциях и практических приложениях, изменяя наше представление о мире и его возможностях.
Практическое применение знания об исключительных случаях в математике

Расширение знаний в области исключительных случаев в математике имеет практическое применение в различных сферах. Рассмотрим несколько примеров, где понимание исключительных ситуаций может быть весьма полезно.
| Сфера применения | Конкретный пример |
|---|---|
| Криптография | В разработке криптографических алгоритмов необходимо учитывать все возможные исключения и рассмотреть случаи, когда обычные математические правила не применимы. Например, при использовании арифметики в конечных полях, необходимо учитывать исключительные случаи, связанные с делением на ноль или генерацией случайных чисел. |
| Финансовая аналитика | |
| Машинное обучение | В разработке алгоритмов машинного обучения, знание об исключительных случаях позволяет учесть граничные значения и строить более стабильные модели. Например, при обработке изображений, необходимо учитывать исключительные случаи, связанные с наличием шумов или артефактов, чтобы заранее предусмотреть соответствующие преобразования. |
Как видно из приведенных примеров, знание об исключительных ситуациях в математике имеет практическое применение в различных областях. Умение учесть исключения и их влияние на результаты анализа или моделирования позволяет получить более точные и надежные результаты.
Вопрос-ответ

Могут ли натуральные числа быть нецелыми?
Нет, натуральные числа всегда являются целыми. Натуральные числа - это положительные целые числа, которые начинаются с единицы и продолжаются бесконечно. Они не могут быть дробными или отрицательными.
Есть ли какие-либо исключения, когда натуральные числа перестают быть целыми?
Нет, натуральные числа всегда остаются целыми. В теории чисел, натуральные числа определены как положительные целые числа без дробной части или показателя. Они не подвержены никаким исключениям, их основные свойства и характеристики сохраняются для всех натуральных чисел.
Что означает быть натуральным числом и почему они не могут быть нецелыми?
Натуральные числа - это первые положительные числа, начинающиеся с единицы и идущие в неопределенность. Они используются для подсчета объектов или итераций. Натуральные числа не могут быть нецелыми, потому что они будут иметь дробную или отрицательную часть, что противоречит их определению. Натуральные числа определены как целые и положительные, и этот набор свойств сохраняется для всех натуральных чисел.



