Окружности являются одним из универсальных объектов геометрии, которые находят применение в различных областях науки и техники. Одной из наиболее интересных задач является изучение окружностей, которые могут быть описаны в равнобедренных треугольниках.
Такие окружности обладают набором уникальных свойств и особенностей, которые позволяют решать разнообразные задачи. Исследование и понимание этих свойств позволяет углубить наши знания о геометрии и расширить нашу способность анализировать различные геометрические фигуры и их свойства.
Применение окружностей в равнобедренных треугольниках имеет широкий спектр возможностей. Это относится как к теоретическим исследованиям, так и к практическому применению в различных областях, таких как инженерия, архитектура, геодезия и другие. Знание и понимание этих свойств окружностей в равнобедренных треугольниках позволяют решать задачи, связанные с определением координат, найденных углов, или же нахождением радиусов и длин дуг этих окружностей.
Основные понятия
В данном разделе мы рассмотрим ключевые термины и определения, связанные с исследованием свойств окружностей в треугольниках, где две стороны равны друг другу. Знание этих понятий позволит нам лучше понять все важные особенности и практическое применение данной темы.
| Термин | Определение |
|---|---|
| Медиана | Прямая линия, соединяющая вершину треугольника и середину противоположной стороны. |
| Высота | Перпендикулярная прямая, проведенная из вершины треугольника к противоположной стороне или ее продолжению. |
| Биссектриса | Прямая, делящая угол треугольника пополам. |
| Центр окружности | Точка, являющаяся центром описанной окружности в треугольнике. |
| Диаметр | Отрезок, соединяющий две точки на окружности и проходящий через ее центр. |
| Ортоцентр | Точка пересечения высот треугольника. |
Понимание этих понятий и их взаимосвязи является важным шагом для изучения свойств окружностей в равнобедренных треугольниках. Оно позволяет нам не только проводить геометрические рассуждения, но и работать с конкретными задачами, которые встречаются в теории и практике.
Уравнение окружности и связь с треугольником с равными сторонами
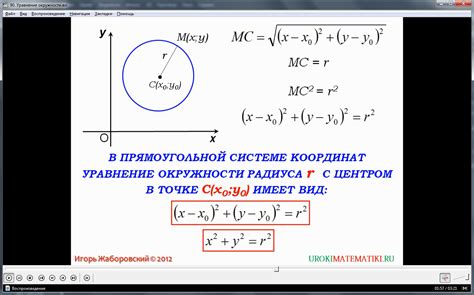
В данном разделе мы рассмотрим связь между уравнением окружности и особенностями равнобедренного треугольника. Разберем, какие параметры окружности могут быть выражены через свойства равнобедренного треугольника, а также как уравнение окружности может помочь в решении задач, связанных с данной темой.
Уравнение окружности является математическим представлением геометрического объекта, который представляет собой множество точек на плоскости, равноудаленных от одной фиксированной точки, называемой центром окружности. Важным параметром уравнения является радиус – расстояние от центра окружности до любой точки на окружности. Уравнение окружности может быть записано в виде (x – a)2 + (y – b)2 = r2, где (a, b) – координаты центра окружности, а r – радиус.
Связь уравнения окружности с равнобедренным треугольником заключается в том, что некоторые параметры окружности могут быть выражены через стороны и углы треугольника. Например, если известны длины сторон треугольника, то радиус окружности, описанной около этого треугольника, может быть выражен через эти стороны с помощью знаменитой формулы Герона.
Знание уравнения окружности и его связь с равнобедренным треугольником позволяют решать различные задачи, связанные с данным геометрическим объектом. Например, нахожение координат центра окружности или радиуса может быть полезным при построении графиков или решении задач, связанных с геометрией или механикой.
Способы создания описанной окружности в равнобедренном треугольнике
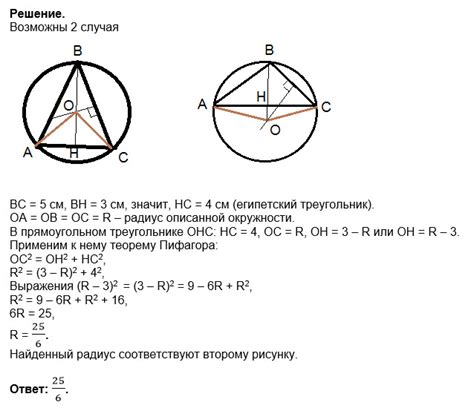
В данном разделе будут рассмотрены различные методы построения описанной окружности в равнобедренном треугольнике, которые помогут нам более полно понять и изучить эту важную особенность и применение в геометрии.
1. Метод углов:
- Найти вершины треугольника, соединить их внутренними углами
- Найти середину основания равнобедренного треугольника и соединить ее с вершинами
- Описанная окружность будет проходить через эти три точки
2. Метод сторон:
- Найти середину основания равнобедренного треугольника и соединить ее с вершиной
- Найти середину боковой стороны равнобедренного треугольника и соединить ее с вершиной
- Перпендикуляр, опущенный из середины боковой стороны на основание, пересекает описанную окружность в точке
3. Метод высот и медиан:
- Найти высоту и медиану равнобедренного треугольника, проведенные из вершины
- Точка пересечения этих линий будет лежать на описанной окружности
Использование этих способов позволяет точно построить описанную окружность в равнобедренном треугольнике и применять ее свойства для решения различных геометрических задач.
Окружность, описанная вокруг треугольника: важности и особенности
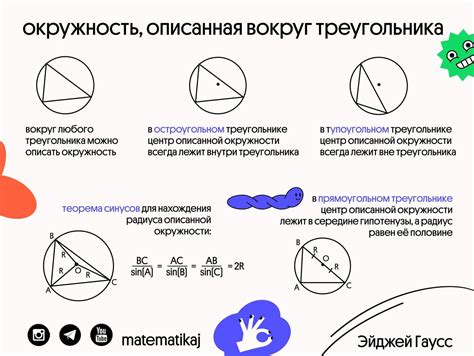
В данном разделе мы рассмотрим особенности и важные свойства окружности, описанной вокруг треугольника. Этот геометрический объект играет значительную роль в изучении треугольников и широко применяется в различных областях математики и физики.
Окружность, описанная вокруг треугольника, представляет собой окружность, которая проходит через все три вершины треугольника. Ее особенности и свойства могут быть использованы для решения разнообразных задач и доказательства теорем, связанных с треугольниками.
Одно из ключевых свойств описанной окружности заключается в том, что ее центр совпадает с пересечением перпендикуляров, проведенных из середин каждой стороны треугольника. Это позволяет нам определить центр окружности и точно построить ее с помощью геометрических построений.
Важной характеристикой описанной окружности является ее радиус. Радиус окружности равен половине длины диаметра, который исходит от центра окружности до любой из ее точек. Таким образом, радиус описанной окружности может быть использован для нахождения других свойств треугольника, таких как его площадь или длины его сторон.
С помощью свойств описанной окружности мы можем также доказать некоторые важные теоремы о треугольниках. Например, теорема о том, что угол, образованный вписанной окружностью и хордой треугольника, равен половине меры дуги этой окружности.
Радиус описанной окружности: расстояние от центра до вершин треугольника
Радиус описанной окружности является важным параметром, который определяет форму и размеры равнобедренного треугольника. От него зависят такие элементы как углы треугольника, длины его сторон, центр тяжести и другие характеристики. Расстояние от центра окружности до вершин треугольника влияет также на его устойчивость при поворотах и перемещениях.
| Свойство | Описание |
|---|---|
| Углы треугольника | Радиус описанной окружности является радиус-вектором для каждой вершины треугольника, что определяет их углы, так как на окружности дуги между вершинами и центром равны. |
| Длины сторон | Радиус описанной окружности связан с длинами сторон равнобедренного треугольника по формуле: \(R = \frac{a}{2\sin\frac{A}{2}}\), где \(R\) - радиус окружности, \(a\) - длина основания треугольника, \(A\) - величина угла при основании. |
| Центр тяжести | Радиус описанной окружности проходит через центр тяжести равнобедренного треугольника, что важно при рассмотрении его динамических свойств и равновесия. |
Применение свойства радиуса описанной окружности находит применение в различных областях, таких как геометрическое моделирование, строительство, компьютерная графика и архитектура. Знание этого свойства позволяет более точно анализировать формы и размеры равнобедренных треугольников и учитывать их особенности при решении конкретных задач.
Ортоцентр и его связь с высотами и описанной окружностью треугольника

Высоты – это линии, проведенные из вершин треугольника к противоположным сторонам под прямым углом. Важно отметить, что ортоцентр всегда лежит на пересечении высот треугольника.
Существует также связь между ортоцентром и описанной окружностью треугольника. Описанная окружность – это окружность, проходящая через все вершины треугольника. Ортоцентр оказывается центром описанной окружности в случае, если треугольник является остроугольным.
Интересно отметить, что для разных типов треугольников связь между ортоцентром и описанной окружностью может проявляться по-разному. Например, для тупоугольного треугольника ортоцентр может оказаться внутри описанной окружности. Эти особенности связи ортоцентра с описанной окружностью открывают новые возможности для изучения треугольников и их свойств.
Таким образом, роль ортоцентра в треугольниках не только заключается в пересечении высот, но также связана с описанной окружностью, открывая интересные зависимости и особенности в геометрии треугольников.
Углы на одной дуге описанной окружности

Когда углы, стоящие на одной дуге описанной окружности в равнобедренном треугольнике, имеют одинаковую меру, мы можем утверждать, что соответствующие углы самого треугольника также равны между собой. Это свойство позволяет нам использовать информацию о мерах углов на дуге для нахождения неизвестных углов треугольника.
Применение кругов, вписанных в равнобедренные треугольники
В предыдущих разделах мы изучили различные свойства кругов, вписанных в равнобедренные треугольники. Теперь рассмотрим, как эти знания можно применить на практике.
| Применение | Описание |
|---|---|
| Геометрическая конструкция | Вписанные окружности являются полезным инструментом для геометрической конструкции различных фигур. Они помогают определить точки пересечения линий, углы и другие характеристики фигур. |
| Решение задач | Применение описанных окружностей в решении геометрических задач позволяет упростить процесс и получить точные результаты. Зная свойства вписанных окружностей, можно легко найти значения углов и отрезков в треугольнике, что полезно при доказательстве или решении других геометрических задач. |
| Строительство | Круги, вписанные в равнобедренные треугольники, могут быть использованы в строительстве. Например, они используются для построения ориентирных точек и выравнивания стен, а также для расчета и установки углов при строительстве крыш. |
| Архитектура | Применение описанных окружностей в архитектуре позволяет создавать более гармоничные и симметричные сооружения. Архитекторы используют эти окружности для определения пропорций и форм зданий, а также для создания впечатляющих фасадов. |
Использование описанных окружностей в различных областях может значительно упростить и улучшить работу. Знание и понимание их свойств позволяет использовать их в качестве помощника при решении геометрических задач, строительстве и дизайне.
Построение треугольника по описанной окружности и двум сторонам
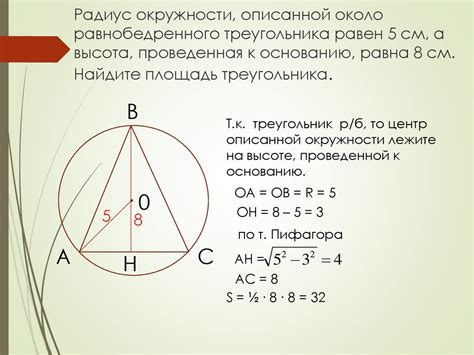
Рассмотрим уникальный метод построения треугольника, основанный на использовании описанной окружности и двух известных сторон. Этот метод позволяет определить размеры и форму треугольника, используя лишь эти данные без необходимости знать углы.
Идея заключается в поиске точки пересечения двух дуг окружности, которые равны заданным сторонам треугольника. После такого поиска, треугольник можно построить, соединяя найденную точку с вершинами, соответствующими известным сторонам.
Построение треугольника по описанной окружности и двум сторонам может применяться в различных сферах, например, в геодезии, архитектуре и машиностроении. Этот метод является эффективным инструментом для определения формы и размеров объектов на основе ограниченного набора известных данных.
Использование свойствы описывающей окружности в решении геометрических задач

Сущность этого свойства заключается в следующем: если в треугольнике есть описанная окружность, то некоторые связанные с ней элементы также будут иметь общие свойства. Например, диаметр описанной окружности всегда проходит через вершину углаой в треугольнике. Это означает, что угол, измеряемый этим диаметром, является прямым.
Использование этого свойства также позволяет связать различные параметры треугольника, такие как радиус описанной окружности, длины сторон и углы в треугольнике. Это позволяет упростить геометрические вычисления и облегчить решение задач, связанных с построением и анализом треугольников.
Вопрос-ответ

Какие свойства имеют окружности, описанные в равнобедренных треугольниках?
Окружности, описанные в равнобедренных треугольниках, имеют несколько важных свойств. Во-первых, центр окружности, описанной в равнобедренном треугольнике, совпадает с точкой пересечения высот треугольника. Во-вторых, радиус этой окружности равен половине высоты треугольника. Также, длина дуги, ограниченной двумя сторонами равнобедренного треугольника и хордой, равна половине периметра треугольника.
Как можно использовать свойства окружностей в равнобедренных треугольниках?
Знание свойств окружностей в равнобедренных треугольниках может быть полезным при решении геометрических задач. Например, можно использовать центр окружности, описанной в равнобедренном треугольнике, чтобы найти точку пересечения высот. Также, радиус этой окружности помогает найти высоту треугольника. А знание длины дуги, ограниченной хордой, может быть полезным при вычислении периметра треугольника.
Можно ли применять свойства окружностей из равнобедренных треугольников в других типах треугольников?
Свойства окружностей, которые применимы в равнобедренных треугольниках, не всегда применимы в других типах треугольников. Например, центр окружности, описанной в равнобедренном треугольнике, может не совпадать с точкой пересечения высот в других типах треугольников. Тем не менее, некоторые свойства окружностей, такие как длина дуги, всегда применимы независимо от типа треугольника.
Как можно доказать свойства окружностей в равнобедренных треугольниках?
Свойства окружностей в равнобедренных треугольниках могут быть доказаны с использованием геометрических доказательств. Например, чтобы доказать, что центр окружности, описанной в равнобедренном треугольнике, совпадает с точкой пересечения высот, можно использовать свойство перпендикулярности. Доказательства могут быть различными в зависимости от конкретных свойств окружностей, но обычно они основаны на применении геометрических правил и свойств треугольников.