Когда мы смотрим на треугольник, наше внимание обычно привлекают его углы и стороны. Треугольники являются элементарными геометрическими фигурами, в которых скрыто множество интересных закономерностей и свойств. Одно из таких свойств заслуживает особого внимания - теорема косинусов.
Теорема косинусов - это мощный инструмент, позволяющий нам вычислять неизвестные стороны или углы прямоугольного треугольника, основываясь только на известных данных. Но что она собой представляет и как она работает?
Узнаваемая по формуле синуса, теорема косинусов опирается на принцип использования косинуса угла между двумя известными сторонами треугольника. Эта формула позволяет нам исследовать отношения между сторонами и углами треугольника и узнать недостающие данные, даже если у нас нет информации о противолежащих углах или сторонах.
За десятилетия исследований и применения в различных областях науки и техники, теорема косинусов зарекомендовала себя как надежный метод для решения разных геометрических задач. К примеру, она широко применяется в астрономии, навигации, геодезии и многих других областях, где точные расчеты и измерения играют важную роль.
Принцип функционирования теоремы косинусов в прямоугольном треугольнике
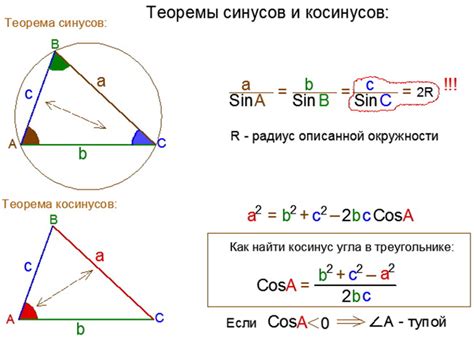
Рассмотрение вопроса о принципе действия теоремы косинусов в прямоугольном треугольнике позволяет углубить наше понимание его сути и значение. Метод основан на использовании математического соотношения, которое позволяет связать длины сторон треугольника с углами между ними. Основной принцип функционирования этой теоремы заключается в использовании синусов и косинусов углов треугольника для нахождения длины его сторон или определения углов при известных сторонах.
Важно отметить, что данный принцип основывается на использовании геометрических свойств треугольника и связи между его сторонами и углами. Он позволяет решать различные задачи, связанные с прямоугольными треугольниками, например, нахождение длины стороны треугольника, определение значения угла между сторонами или определение существования прямого угла в треугольнике.
При использовании принципа работы теоремы косинусов важно учитывать, что ее эффективность напрямую зависит от правильного определения углов и соответствующей выборки соответствующих сторон треугольника. Однако, при правильном применении принципа, можно достичь высокой точности результатов и востребованности этого метода в практических задачах.
Основы теоремы косинусов
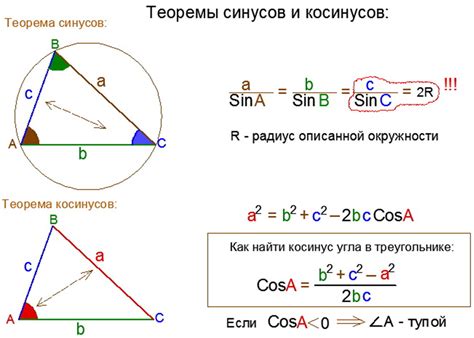
Перед тем как перейти к более детальному объяснению, давайте рассмотрим общую идею, которая лежит в основе этой теоремы. Она позволяет нам находить зависимость между длинами сторон треугольника и углами, которые образуют эти стороны. Таким образом, теорема косинусов позволяет нам решать задачи, в которых необходимо найти длину или угол треугольника, если известны другие значения.
Для полного понимания теоремы косинусов, нам необходимо изучить саму формулу, которая позволяет нам вычислить длину одной из сторон треугольника. Формула выражает зависимость между длиной стороны треугольника, двумя другими сторонами и углом между ними. Эта формула имеет универсальное применение и позволяет нам решать широкий спектр задач, связанных с треугольниками.
Примеры применения и практическое использование теоремы косинусов

Различные области и науки нашли применение теоремы косинусов в своей практике, используя ее для решения разнообразных задач и расчетов. Полученные результаты позволяют определить значения неизвестных величин или углов в разноплановых ситуациях, где известны длины сторон и/или углы в прямоугольном треугольнике.
| Область применения | Примеры использования |
|---|---|
| Геодезия | Расчет расстояний и направлений между точками на поверхности Земли. |
| Физика | Определение сил, действующих на тело в трехмерном пространстве. |
| Архитектура | Расчет длин, высот и углов зданий для определения их устойчивости и конструктивной целостности. |
| Навигация | Определение координат и направления движения объектов на море, в воздухе или на суше. |
| Космонавтика | Расчет траекторий полетов и определение силы притяжения для навигации и управления космическими аппаратами. |
Примеры применения теоремы косинусов в указанных областях подтверждают ее эффективность и адаптивность к различным ситуациям. Без использования этой теоремы, многие расчеты и измерения стали бы гораздо сложнее и менее точными, поэтому она является важным инструментом для ученых, инженеров и специалистов в различных областях деятельности.
Алгоритм решения проблемы неизвестных сторон и углов в треугольнике

В данном разделе будет представлен алгоритм расчета сторон и углов треугольника с использованием основных принципов и формул геометрии. При помощи этих методов можно с высокой точностью определить все неизвестные значения треугольника, основываясь на заданных параметрах.
В первую очередь, для определения неизвестных сторон и углов в треугольнике мы воспользуемся теоремой косинусов, которая позволяет найти значение любой стороны или угла треугольника при условии, что известны длины двух других сторон или, соответственно, значения двух других углов.
Для начала выберем известные данные, такие как известные стороны и углы треугольника, которые мы можем использовать для расчета отсутствующих значений. Затем, применяя теорему косинусов, мы определим формулы для вычисления отсутствующих сторон и углов треугольника, используя известные данные.
Для расчета сторон треугольника мы используем формулу косинусов, которая говорит нам, что квадрат стороны равен сумме квадратов двух других сторон, умноженных на два произведения этих сторон на косинус соответствующего им угла.
Аналогично, для вычисления углов треугольника мы используем обратную формулу косинусов, которая позволяет найти степень угла, основываясь на длинах сторон треугольника и известном значении косинуса данного угла.
Применяя эти формулы и алгоритмы, мы можем эффективно решить проблему неизвестных значений в треугольнике, получив информацию о его сторонах и углах, основываясь на заданных параметрах.
- Выберите известные данные треугольника
- Примените теорему косинусов для нахождения формул расчета отсутствующих сторон треугольника
- Используйте обратную формулу косинусов для вычисления углов треугольника
- Произведите расчеты, используя полученные формулы и известные данные
- Проверьте результаты расчетов и полученные значения
Вопрос-ответ

Какую задачу решает теорема косинусов в прямоугольном треугольнике?
Теорема косинусов позволяет найти любую из сторон треугольника, если известны длины двух других сторон и между ними заключенный угол.
Какая формула используется для применения теоремы косинусов в прямоугольном треугольнике?
Для применения теоремы косинусов в прямоугольном треугольнике используется формула: c^2 = a^2 + b^2 - 2ab*cos(угол C), где c - гипотенуза, a и b - катеты, угол C - угол между гипотенузой и одним из катетов.
Как можно применять теорему косинусов в практических задачах?
Теорема косинусов может быть полезна в решении различных задач, например: определение расстояния между двумя точками на плоскости, нахождение высоты треугольника, определение углов треугольника по длинам его сторон. В каждой задаче необходимо определить известные данные и применить формулу теоремы косинусов для нахождения неизвестной величины.
Какая эффективность теоремы косинусов в прямоугольном треугольнике?
Теорема косинусов является одним из основных инструментов для решения задач, связанных с прямоугольными треугольниками. Она позволяет находить неизвестные величины с высокой точностью и применяется в различных областях, таких как геометрия, оптика, астрономия и многих других. Эффективность теоремы косинусов заключается в её простоте использования и широких возможностях решения разнообразных задач.



