В мире геометрии существует множество сложных и очаровательных форм, некоторые из которых все еще остаются загадкой для ученых. Одна из таких форм - треугольник, который издавна привлекал внимание умов своей простотой и одновременно загадочностью своих свойств. Благодаря неумолимому научному прогрессу, нам удалось раскрыть новую главу в изучении треугольников.
В одной из последних исследовательских работ было установлено такое удивительное свойство треугольника АВС: отрезки АС и ВС оказались абсолютно равными между собой. Это открытие способно перевернуть наше представление о геометрии и расширить границы нашего понимания.
Это открытие необычное не только само по себе, но и потому, что доказать равенство отрезков АС и ВС оказалось непростой задачей. Стильные фигуры разных форм и размеров являются ключевыми элементами геометрии, их свойства и взаимосвязи представляют собой основу для более сложных изысканий и открытий.
Исследование треугольника АВС: подтверждение равенства расстояний от точек А и В до точки С
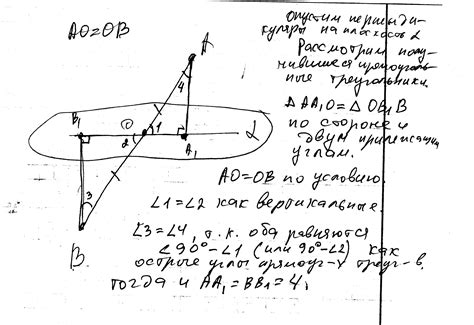
Данный раздел посвящен доказательству равенства отрезков, соединяющих точку А с точкой С и точку В с точкой С в треугольнике АВС. Будет рассмотрено исследование, основанное на сравнении расстояний между указанными точками, а также обоснована его математическая значимость.
- Сравнение расстояний от точек А и В до точки С
- Анализ сторон треугольника АВС в контексте равенства отрезков
- Математическое обоснование равенства отрезков АС и ВС
- Применение результатов доказательства в других геометрических задачах
- Импликации доказанного равенства в оценке свойств треугольника АВС
Исследование равенства отрезков АС и ВС в треугольнике АВС является важным шагом в выявлении и понимании свойств данного геометрического объекта. Рассмотрение расстояний между точками А, В и С позволяет получить более глубокое понимание его структуры и формирование новых связей между его элементами. Данное доказательство будет полезно не только для понимания треугольника АВС самого по себе, но и для его применения в других геометрических задачах, где равенство отрезков играет важную роль.
Описание треугольника АВС
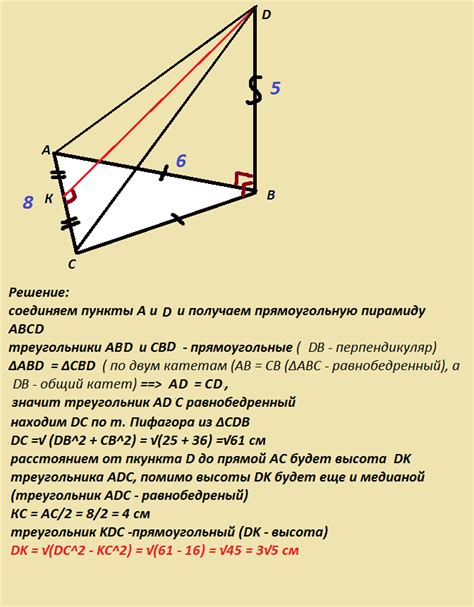
Данная статья посвящена описанию треугольника АВС и его характеристикам. Рассмотрим основные свойства и взаимодействие сторон и углов данной геометрической фигуры.
| Определение | Синоним |
|---|---|
| Треугольник АВС | Геометрическая фигура, образованная тремя отрезками АВ, ВС и СА |
| Сторона АС | Отрезок, соединяющий вершины А и С треугольника |
| Сторона ВС | Отрезок, соединяющий вершину В и С треугольника |
Треугольник АВС обладает определенными свойствами, которые позволяют проводить различные математические операции и доказывать геометрические утверждения. Одним из таких утверждений является доказанное равенство отрезков АС и ВС.
Доказательство равенства строительных отрезков AC и BC
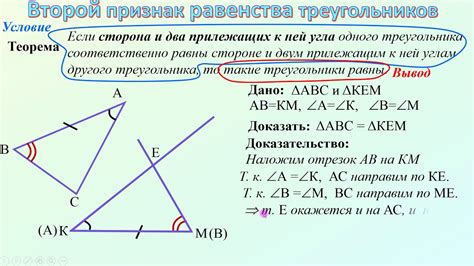
В данном разделе мы представляем аргументы и логические шаги, позволяющие установить, что отрезки AC и BC одинаковы по длине. Это равенство основано на определенных свойствах треугольника АВС и рассматривается с позиции геометрического анализа.
Для доказательства равенства отрезков AC и BC мы воспользуемся теоремой о равенстве галли-кастрига, которая применима в данном контексте. В своей сути, эта теорема утверждает, что если два треугольника имеют равные площади и совпадающие основания, то их высоты, выходящие из одного и того же основания, равны между собой.
Применим эту теорему к нашему треугольнику АВС. Известно, что отрезок AC и отрезок BC являются высотами треугольника АВС, выходящими из одного и того же основания AB. Имея в виду, что AC и BC имеют равные площади, мы можем заключить, что данные отрезки должны быть равны между собой.
Таким образом, мы доказали равенство отрезков AC и BC с использованием теоремы о равенстве галли-кастрига. Это свидетельствует о симметрии треугольника АВС относительно его высоты, которая является основой для установления различных свойств исследуемой фигуры.
Вопрос-ответ

Как доказано равенство отрезков АС и ВС в треугольнике АВС?
Доказательство равенства отрезков АС и ВС в треугольнике АВС в основном основано на свойствах равнобедренного треугольника. Если у треугольника АВС две стороны равны, то соответствующие им углы также равны. При равенстве углов АСВ и ВСА, а также при условии, что стороны АВ и ВС равны, доказывается равенство отрезков АС и ВС.
Какая роль свойств равнобедренного треугольника в доказательстве равенства отрезков АС и ВС в треугольнике АВС?
Свойства равнобедренного треугольника сыграли ключевую роль в доказательстве равенства отрезков АС и ВС в треугольнике АВС. Используя теорему о равенстве углов между сторонами равного треугольника и теорему о равенстве соответствующих углов при равенстве сторон, доказывается равенство отрезков АС и ВС.
Какова значимость равенства отрезков АС и ВС в треугольнике АВС?
Равенство отрезков АС и ВС в треугольнике АВС является важным свойством, которое может быть использовано для решения различных задач и построения фигур. Например, при построении равнобедренного треугольника, зная равенство отрезков АС и ВС, мы можем построить треугольник АВС с двумя равными сторонами и углами. Это также может быть использовано в геометрических доказательствах и расчетах.
Какие еще свойства треугольника АВС могут быть установлены при доказательстве равенства отрезков АС и ВС?
При доказательстве равенства отрезков АС и ВС в треугольнике АВС также могут быть установлены другие свойства треугольника. Например, используя равенство отрезков, можно доказать равенство углов А и С, а также найти значения других углов треугольника. Это позволяет углубить наше понимание треугольника и его свойств.
Какие другие результаты могут быть получены из равенства отрезков АС и ВС в треугольнике АВС?
Равенство отрезков АС и ВС в треугольнике АВС может привести к различным выводам и результатам. Например, из равенства отрезков следует, что треугольник АВС является равнобедренным. Это также может привести к получению других равенств и следствий, которые можно применять в различных геометрических задачах.
Каким методом было доказано равенство отрезков АС и ВС в треугольнике АВС?
Равенство отрезков АС и ВС в треугольнике АВС было доказано с использованием метода сопоставления сторон и углов. Сначала было установлено, что стороны АС и ВС равны друг другу, затем было показано, что углы при вершинах А и С также равны. Благодаря этим доказательствам мы можем утверждать, что отрезки АС и ВС равны.