В мире геометрии существует утверждение, занимающее особое положение - равенство площадей фигур. Этот принцип, как верная аксиома математики, разрешает различные задачи и споры, вызывая интерес ученых, исследователей и просто любителей точных наук. В данной статье мы представим интересные аспекты и новые доказательства этого утверждения, а также приведем захватывающие примеры, подкрепляющие его справедливость.
Рассмотрение области геометрии, в которой площадь является центральным понятием, предполагает учет разнообразных геометрических фигур. Однако, равенство площадей - это не только простое сравнение числовых значений. Здесь требуется более глубокое понимание геометрических свойств и закономерностей, чтобы достичь полного понимания этой концепции. Также важно уяснить, что равные площади олицетворяются разнообразными объектами, относящимися к самым разным сегментам математики.
Такой подход требует аккуратных доказательств и удивительных примеров, которые подчеркнут все грани и области применимости данного утверждения. Ведь математика - не только наука, она также носит некий эстетический характер и способна вызвать эмоции. Именно поэтому в нашей статье мы пройдем путь от простых геометрических фигур до сложных комбинаций, подчеркивая красоту и важность равенства площадей и возводя его в ранг неотъемлемого элемента общей картине математического мира.
Три вида доказательств равенства площадей треугольника и прямоугольника
В данном разделе рассмотрим три различных подхода к доказательству равенства площадей треугольника и прямоугольника. Каждый из этих методов основан на определенных свойствах геометрических фигур и позволяет убедительно доказать данное равенство.
- Метод подсчета площади: В этом методе мы используем известные формулы для вычисления площади треугольника и прямоугольника. Для треугольника применяется формула "половина произведения основания на высоту", а для прямоугольника - "произведение длины на ширину". Путем правильного выбора соответствующих значений основания, высоты, длины и ширины, мы демонстрируем, что оба выражения равны и, следовательно, площади треугольника и прямоугольника равны.
- Метод разбиения фигур: В этом методе мы разбиваем исходную геометрическую фигуру на несколько более простых и понятных частей, таких как треугольники и прямоугольники. Затем мы доказываем равенство площадей этих частей, используя уже известные методы. Наконец, объединяя площади частей, мы приходим к равенству площадей исходной треугольной и прямоугольной фигур.
- Метод конкретного примера: В этом методе мы рассматриваем конкретный пример треугольника и прямоугольника, значения сторон или углов которых выбраны таким образом, что площади совпадают. Мы выясняем, какие особенности и свойства этих фигур приводят к равенству площадей. После этого мы проводим обобщение полученных результатов на общий случай и демонстрируем, что равенство площадей треугольника и прямоугольника верно в общем смысле.
Таким образом, мы видим, что равенство площадей треугольника и прямоугольника может быть убедительно доказано различными способами. Каждый из этих методов требует грамотного применения геометрических свойств и тщательных вычислений, чтобы достичь требуемого результата. Используя данные методы, можно удостовериться в равенстве площадей данных геометрических фигур и расширить свои знания в области геометрии.
Метод сравнения площадей и соотношение размеров фигур
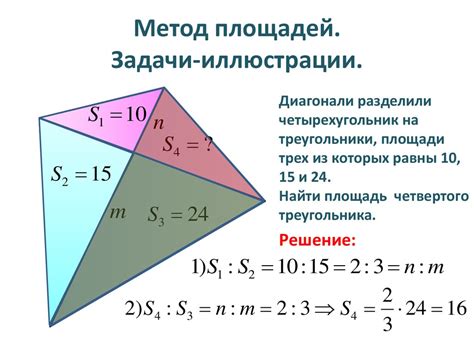
Суть подобия фигур заключается в равенстве углов и пропорциональном соотношении их сторон. Если две фигуры имеют одинаковые углы и соотношение длин сторон, то они считаются подобными. При этом масштабные коэффициенты площадей их представлений будут равны.
- При сравнении площадей фигур можно использовать соответствующие отношения и подсчитывать площадь одной фигуры относительно другой.
- Сравнение площадей фигур также позволяет установить, какая из них больше или меньше другой.
- Исходя из подобия фигур, можно определить долю фигуры относительно другой и выразить это в процентах.
Метод площадей и подобия фигур широко применяется в геометрии и позволяет не только установить равенство площадей, но и анализировать и сравнивать различные геометрические фигуры. Этот метод является надежным и универсальным инструментом для изучаемой проблемы и может быть использован как в доказательствах, так и в практических примерах.
Практические примеры с использованием теоремы
Практические примеры с применением теоремы о равенстве площадей фигур позволят нам увидеть, как данная теория может быть использована для решения конкретных задач. Например, можно рассмотреть ситуацию, когда у нас есть два треугольника с равными сторонами, и нужно установить равны ли их площади или нет. Для этого можно применить теорему о равенстве площадей фигур, а затем использовать известные формулы для нахождения площади треугольника.
- Еще одним примером использования теоремы может быть сравнение площадей различных многоугольников. Например, если у нас есть два прямоугольника с равными периметрами, то с помощью описанной теоремы мы можем установить, равны ли их площади или нет. Для этого необходимо будет провести доказательство и применить формулу для нахождения площади прямоугольника.
- Также теорема о равенстве площадей фигур может быть применена для решения задач связанных с площадью круга. Например, если у нас есть два круга с равными диаметрами, то с помощью данной теоремы мы можем установить, равны ли их площади или нет. Для этого нужно провести доказательство и применить известную формулу для нахождения площади круга.
Соотношение площадей окружности и прямоугольника
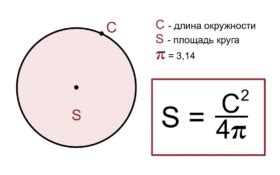
Окружность - это геометрическая фигура, состоящая из всех точек плоскости, равноудаленных от одной фиксированной точки, называемой центром. Прямоугольник - это четырехугольник, у которого все углы прямые.
Сравнивая площадь окружности и прямоугольника, можно заметить, что у них различная форма и структура. Окружность имеет округлую форму, а прямоугольник - прямые углы и ровные стороны. Из-за этого, в общем случае, площади этих фигур будут отличаться друг от друга.
| Фигура | Описание | Формула для вычисления площади |
|---|---|---|
| Окружность | Геометрическая фигура с равноудаленными от центра точками | S = π * r2 |
| Прямоугольник | Четырехугольник со сторонами, образующими прямые углы | S = a * b |
Однако, в особых случаях, существуют специальные отношения между площадями окружности и прямоугольника. Например, если вписать окружность в прямоугольник таким образом, чтобы диаметр окружности был равен одной из сторон прямоугольника, то площадь окружности окажется равной площади этого прямоугольника.
Таким образом, понимание соотношения площадей окружности и прямоугольника требует анализа и сравнения их свойств и структуры. Это позволяет нам лучше понять, как различные геометрические фигуры соотносятся между собой и какие законы и принципы лежат в их основе.
Геометрическое значение числа пи: необычные свойства окружности

Окружность, вписанная в квадрат, является примером геометрической формы, которая связана с числом пи. При увеличении стороны квадрата, радиус окружности также увеличивается, однако отношение длины окружности к диаметру всегда остается постоянным и равным числу пи. Это свойство числа пи можно использовать в различных геометрических задачах и вычислениях.
- Одной из особенностей числа пи является его иррациональность, то есть невозможность представления его десятичной дробью или конечным числом цифр. Это означает, что величина числа пи не может быть точно измерена или выражена с помощью обычных чисел, и она всегда будет содержать бесконечное количество цифр после десятичной точки.
- Число пи также имеет бесконечную десятичную дробь без повторяющихся цифр, что делает его иррациональным и трансцендентным числом. Это означает, что пи не может быть корнем никакого алгебраического уравнения с рациональными коэффициентами и его значения нельзя выразить с помощью конечного числа арифметических операций.
- Каждая цифра числа пи несет информацию о геометрических свойствах окружности. Например, первая цифра пи 3 указывает на то, что длина окружности в 3 раза больше ее диаметра. Вторая цифра пи 1 указывает на то, что окружность может поместиться внутри квадрата, чья сторона равна 1. Третья цифра пи 4 указывает на соотношение между площадью круга и площадью квадрата, вписанного в него. И так далее.
Геометрическая интерпретация числа пи позволяет увидеть связь между математикой и физическим миром. Она является важной основой для дальнейшего изучения геометрии, тригонометрии и развития математического мышления.
Примеры из повседневной жизни, демонстрирующие одинаковые площади

В нашей повседневной жизни часто встречаются ситуации, где различные объекты или области имеют одинаковые площади. Такие примеры помогают наглядно понять и убедиться в том, что площади фигур могут быть равными. Рассмотрим несколько примеров из различных областей нашей жизни.
| Примеры | Описание |
|---|---|
| Квадратная комната и прямоугольная комната | Площадь квадратной комнаты со сторонами 5 метров будет равна площади прямоугольной комнаты с шириной 2,5 метра и длиной 10 метров. |
| Круглый стол и прямоугольный стол | Площадь круглого стола диаметром 1 метр будет равна площади прямоугольного стола с шириной 1 метр и длиной 3,14 метра. |
| Треугольный участок и прямоугольный участок | Площадь треугольного участка с основанием 4 метра и высотой 2 метра будет равна площади прямоугольного участка с шириной 2 метра и длиной 4 метра. |
| Цветочная грядка и газон | Площадь цветочной грядки длиной 3 метра и шириной 2 метра будет равна площади газона с длиной 6 метров и шириной 1 метр. |
Эти примеры подтверждают, что площади фигур могут быть равными даже при различной форме или размерах. Это демонстрирует принцип равенства площадей и подтверждает верность утверждения о равенстве площадей различных фигур. Знание и применение этого принципа имеет практическую значимость во многих областях, от архитектуры до торговли недвижимостью.
Вопрос-ответ

На сколько важно доказать равенство площадей фигур?
Доказание равенства площадей фигур является важным шагом при решении геометрических задач. Оно позволяет установить соответствия между различными фигурами и использовать их свойства для получения новых результатов.
Какие методы можно использовать для доказательства равенства площадей фигур?
Для доказательства равенства площадей фигур можно использовать различные методы, включая методы подсчета площадей, методы подобия фигур, методы использования свойств геометрических фигур и теорем. Кроме того, можно применять алгебраические методы и математическую индукцию.
Какими свойствами можно пользоваться для доказательства равенства площадей фигур?
Для доказательства равенства площадей фигур можно использовать такие свойства, как равенство геометрических фигур по наличию равных сторон или углов, равенство площадей фигур с помощью разбиения на более простые фигуры, равенство площадей фигур при подобии и симметрии и другие свойства геометрических фигур.
Что такое примеры равенства площадей фигур?
Примеры равенства площадей фигур представляют собой конкретные геометрические фигуры, для которых доказано равенство их площадей. Эти примеры являются показательными и помогают лучше понять методы доказательства равенства площадей фигур.
Какие фигуры могут быть равными по площади?
Фигуры могут быть равными по площади, если они имеют одинаковую площадь, то есть количество единичных квадратных единиц, которыми можно заполнить каждую из этих фигур, совпадает. Например, два прямоугольника могут быть равными по площади, если их длины и ширины соответственно равны.



