В самом сердце геометрии скрыты величина и симметрия, порождающие удивительные формы. Одной из них является куб – одна из наиболее известных трехмерных фигур, обладающая своей уникальностью и привлекательностью.
Начнем наше путешествие по миру куба с его вершин. Они являются непременными элементами фигуры, точками схода и развилки всех граней. Вершины куба задают его форму, определяют его устойчивость и делают его неповторимым. Каждая вершина куба взаимодействует с другими, образуя совершенно уникальное пространство.
Вместе с вершинами, грани составляют структуру куба и придают ему еще больше геометрической красоты. Грани куба являются его боковыми поверхностями, охватывающими его объем. Они обладают своей шириной, высотой и глубиной, создавая иллюзию глубины и перспективы. Каждая грань имеет свой цвет, свою текстуру, свою энергию, делая куб многогранным и загадочным.
Особенности и структура вершин квадрата
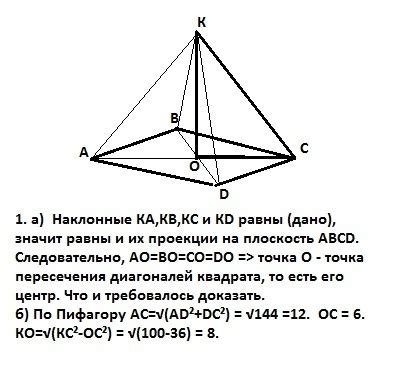
Вершины куба представляют собой точки, где пересекаются три ребра, образуя углы. Они являются крайними точками конструкции и важнейшими компонентами для определения геометрической формы куба. Каждая вершина куба обладает своими особенностями и связями с остальными элементами конструкции.
Вершина - это не только визуальный элемент куба, но и ключевой фактор в его прочности и устойчивости. За счет правильного распределения нагрузок, вершины куба способны выдерживать внешние воздействия и поддерживать его целостность. Они также служат точками для соединения ребер и образуют основу для определения граней, таким образом направляя конструкцию и придавая ей особую структуру.
Имея ломаную форму, вершины куба создают трехмерное пространство и визуально отображают его. Они придают кубу эстетичность и симметрию, позволяя нам воспринимать его как цельную и гармоничную геометрическую фигуру.
Вершина куба: измерение точки пересечения углового множества
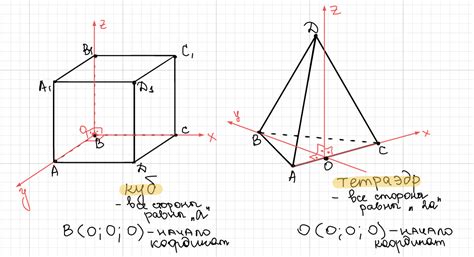
Такая точка является инициатором для образования других элементов фигуры, которые основаны на ее координатах. Она выступает в роли отправной точки для построения других отрезков и связей внутри фигуры. Вершина куба расположена на перекрестке трех граней и двух ребер, что придает ей важность и уникальность в геометрии.
Основной характеристикой вершины является ее местоположение в пространстве. Оно определяется через значения координат, которые могут быть представлены числами или символами. Также важными аспектами являются углы, под которыми пересекаются грани и ребра куба, их взаимное расположение и соединения.
Кроме того, вершина куба может быть характеризована своими визуальными свойствами, такими как цвет, текстура или отражение света. Эти атрибуты вносят дополнительные аспекты в описание и идентификацию вершины, позволяя ей выделяться среди других элементов фигуры.
Уникальный раздел: "Особенности вершины куба"

Каждая вершина куба представляет собой точку пересечения трех ребер. Они обеспечивают жесткую связь между гранями, придавая кубу его устойчивость и уникальность в пространстве.
| Особенности вершины куба |
|---|
| 1. Уникальность |
| 2. Компактность |
| 3. Жесткость |
| 4. Устойчивость |
Вершины куба играют важную роль в его геометрии и механике. Они также позволяют кубу становиться базовым строительным блоком для создания различных геометрических форм. Благодаря своим особенностям, вершины куба помогают в создании прочных и устойчивых конструкций.
Грани куба
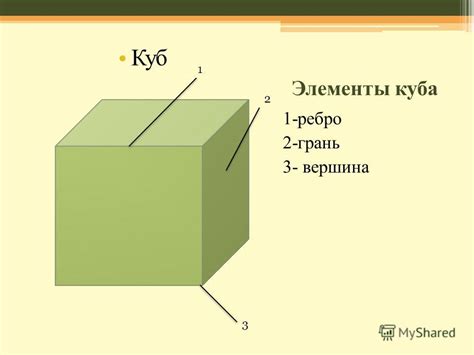
Этот раздел посвящен описанию и особенностям плоских сторон многогранника, образующего трехмерную фигуру.
- Стороны куба являются плоскими поверхностями, заключающими в себе весь объем фигуры.
- Грани куба обладают одинаковыми размерами, формой и ориентацией.
- Каждая грань куба является квадратом, ограниченным четырьмя прямыми сторонами.
- Куб имеет шесть граней, причем каждая грань имеет по две смежные грани.
- Грани куба расположены под прямыми углами друг к другу, образуя пересечения в виде ребер.
- Четыре грани куба находятся на его боковых сторонах, а две другие грани являются верхней и нижней плоскостями.
Грани куба являются одним из основных элементов его структуры, обладая своими характеристиками и отношениями с окружающим пространством. Изучение граней куба позволяет понять особенности его формы и визуального восприятия. Благодаря своей симметрии и регулярности, грани куба находят широкое применение в различных областях, включая геометрию, архитектуру, компьютерную графику и дизайн.
Характеристики стороны куба
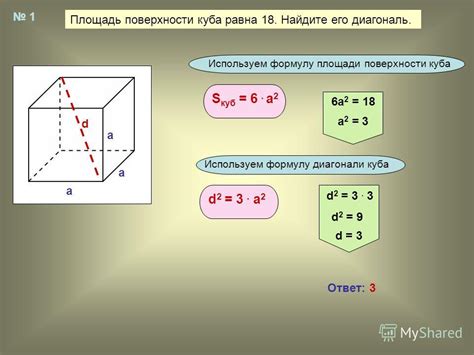
В данном разделе рассматриваются особенности одной из основных составляющих геометрической формы. При рассмотрении стороны куба мы погрузимся в узнавание уникальных свойств этого плоского элемента.
Одна из поверхностей, которая образует грани куба, имеет свои особенности и характеристики, которые определяют ее отличительные черты. Каждая сторона, будучи грани куба, отличается своей формой, размером, ориентацией и расположением относительно других сторон.
Боковая сторона, являясь одной из граней куба, отличается от других граней своими геометрическими особенностями. Стоит отметить, что боковые стороны куба являются прямоугольниками и плоскими элементами, которые имеют одинаковые размеры и формы.
Изучение различных характеристик стороны куба поможет нам полнее понять уникальность этой геометрической фигуры и ее важное значение в математике и геометрии. Каждая сторона куба демонстрирует свои особенности, которые отличают ее от других элементов и придают уникальность этой геометрической форме.
Особенности поверхности куба
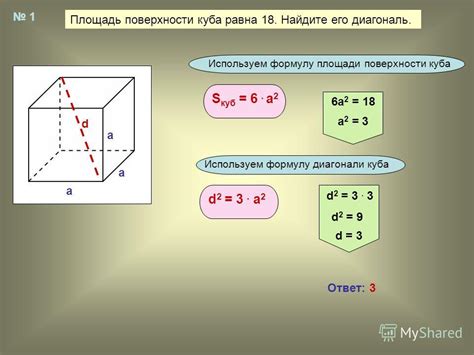
Первая особенность грани куба – это ее форма, которая, как и у самого куба, представляет собой прямоугольник. Поскольку куб имеет шесть граней, каждая из них является прямоугольной поверхностью, состоящей из четырех прямых углов и четырех сторон.
Кроме формы, грани куба различаются также по своей ориентации в пространстве. Некоторые грани являются горизонтальными, располагаясь параллельно плоскости земли, в то время как другие грани вертикальны, направлены вверх или вниз.
Каждая грань куба также отличается своей положительной или отрицательной ориентацией относительно других граней. Например, одна грань может быть направлена внутрь куба, обращенная от зрителя, а другая грань может быть направлена наружу, обращенная к зрителю.
Эти особенности граней куба играют важную роль в его структуре и визуальном восприятии. Они определяют форму и ориентацию куба, придают ему уникальность и интересную внешность.
Стороны геометрической фигуры

Представим себе конструкцию, обладающую искривленными линиями, углами и соединениями. Каждая часть этой формы имеет особое назначение и важность. Сегодня мы обратим особое внимание на эти подчастей, которые помогают создать уникальный облик и функциональность данного объекта.
Говоря о геометрической форме, нельзя обойти вниманием ее стороны. Стороны играют важную роль в организации и упорядочении элементов формы.
| Часть | Описание |
|---|---|
| Сторона | Это одно из элементарных понятий, описывающих форму. Сторона – это линия-граница, противостоящая другой стороне и соединяющая две вершины. Стороны куба помогают ему сохранять свою геометрическую форму и служат опорой для других подчастей. |
Особенности линии, соединяющей две точки куба
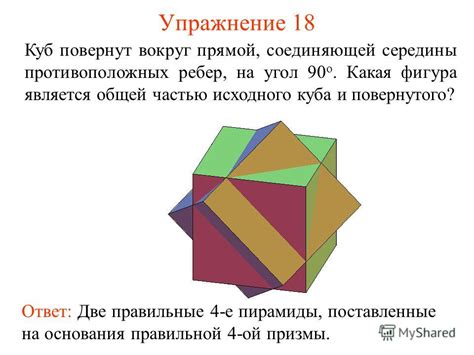
Размер и форма ребра куба зависит от длины ребра и расположения окружающих граней и вершин. Ребра куба являются прямыми и параллельными друг другу, образуя симметричную структуру. Они могут быть представлены различными материалами и иметь разный оттенок, что делает их заметными и отличимыми от других элементов куба.
Ребра куба также обладают свойствами прямой линии, такими как равенство длин и отсутствие изгибов. Благодаря этим характеристикам, ребра позволяют определить форму и размеры куба, а также служат основой для расчетов и построений.
Особенности ребра куба
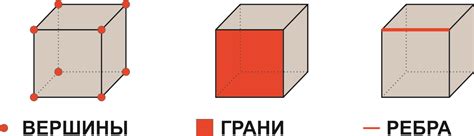
Первым значимым аспектом ребра куба является его длина. Она определяет масштаб и размеры кубической формы. Длина ребра влияет на общую объемную вместительность и возможности использования куба, а также на его визуальное восприятие.
Другим важным свойством ребра куба является его прямота. Ребро является прямой линией, которая соединяет вершины и формирует грани. Прямота ребра обеспечивает геометрическую точность куба и его устойчивость в пространстве.
Кажущаяся однородность ребра обманчива, потому что данная линия имеет две различные стороны. В одной из них происходит внутренняя конструкция куба, а в другой стороне ребра часто находятся маркировки, указывающие на его длину и ориентацию.
Также ребро куба является границей между двумя гранями. Оно придает кубу структуру и форму, обеспечивая его сборку и удержание конкретной позиции в пространстве. Ребро служит основой для расчета объема куба и определения его параметров.
В итоге, ребро куба имеет ключевое значение как строительный элемент, образующий основу для размещения вершин и граней. Его особенности влияют на общую прочность, стабильность и визуальное восприятие кубической формы.
| Особенности ребра куба |
|---|
| Длина |
| Прямота |
| Две различные стороны |
| Граница между гранями |
Вопрос-ответ

Каковы особенности вершины куба?
Вершина куба является точкой, где сходятся три ребра. Куб имеет восемь вершин, которые обозначаются буквами A, B, C, D, E, F, G, H. Каждая вершина куба имеет три смежные вершины.
Что представляют из себя грани куба?
Грани куба - это плоские поверхности, образованные при соединении четырех смежных ребер. Куб имеет шесть граней: верхнюю, нижнюю, переднюю, заднюю, левую и правую грани. Грани куба являются квадратами рангом 2.
Сколько ребер имеет куб?
Куб имеет двенадцать ребер, которые образуют его структуру. Каждое ребро куба соединяет две смежные вершины и является отрезком прямой.
Каковы свойства и характеристики ребра куба?
Ребро куба является отрезком прямой, соединяющим две смежные вершины. Все ребра куба имеют одинаковую длину и они параллельны друг другу. Длина ребра куба может быть вычислена как расстояние между двумя смежными вершинами.
Какие еще особенности и свойства характеризуют куб?
Куб - одна из пяти платоновских тел. Он обладает рядом особенностей: все его грани являются квадратами, все его вершины имеют одинаковую величину углов и сумма всех его углов равна 360 градусов. Куб симметричен относительно центра и может быть вписан в сферу таким образом, что все его вершины будут находиться на поверхности сферы.
Как описать вершину куба?
Вершина куба - это точка пространства, в которой сходятся три ребра куба. Она обозначается обычно буквой V.



