В изучении и решении уравнений и систем уравнений одним из ключевых моментов является поиск значения Х, при котором преобразованная функция обращается в ноль. Это является важным шагом в решении широкого спектра математических проблем, включая физические расчеты, оптимизацию процессов и построение моделей.
В данном контексте значение Х можно рассматривать как некую "ключевую фразу", которая открывает возможность понять и анализировать конкретную ситуацию. Когда мы находим значение Х, при котором преобразованная функция обращается в ноль, мы устанавливаем точку пересечения графика с осью Х, что позволяет нам определить особые точки или важные значения для исследуемой системы.
Значение, при котором функция в степенной степени обращается в нуль: решения и примеры
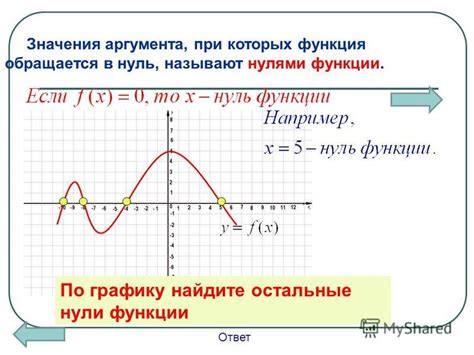
Для нахождения таких значений мы можем применять методы решения уравнений и методы графического анализа. Один из методов – применение индексов степени для определения количества корней уравнения. Другой – использование производной функции для выявления стационарных точек и экстремумов. Какими бы ни были методы, они помогают нам найти значения, которые при подстановке в исходную функцию дают результат ноль.
Рассмотрим пример, чтобы проиллюстрировать этот процесс. Представим функцию f(x) = x^3 - 4x^2 + 4x. Чтобы найти значение, при котором функция обращается в ноль, мы можем использовать метод индексов степеней. Нам нужно определить количество корней уравнения x^3 - 4x^2 + 4x = 0.
Применим индексы степеней: коэффициент перед самой высокой степенью, в данном случае перед x^3, равен 1, а перед оставшимися переменными их степень равна нулю. Исходя из этого, мы можем установить, что у уравнения существует 1 корень.
Используя графический анализ, мы можем построить график функции и наблюдать, где функция пересекает ось абсцисс и обращается в нуль. В данном примере наша функция имеет горизонтальный асимптот в x = 4. Это означает, что значение 4 является значением, при котором функция в степенной степени равна нулю.
Определение корней полинома
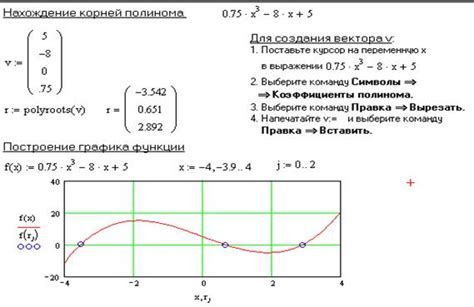
Определить значения переменной, при которых полином равен нулю, позволяет анализ уравнения, его дискриминант, коэффициенты и структура. Знание корней полинома имеет большое значение в различных областях, таких как математика, физика, экономика и другие.
| Пример | Описание |
|---|---|
| Полином 2x^2 - 5x + 3 | В этом примере полином имеет два корня, равные x = 1 и x = 1.5. Они определяются путем решения уравнения 2x^2 - 5x + 3 = 0. |
| Полином x^3 - 9x^2 + 18x - 8 | В данном случае полином имеет три корня, равные x = 1, x = 2 и x = 4. Они могут быть получены путем решения уравнения x^3 - 9x^2 + 18x - 8 = 0. |
| Полином 4x^2 + 12x + 9 | В этом примере полином имеет один корень, равный x = -1.5. Этот корень можно определить как решение уравнения 4x^2 + 12x + 9 = 0. |
Корни полинома являются важными точками, они отражают пересечение графика полинома с осью абсцисс. Знание этих значений позволяет анализировать поведение функции и решать различные задачи, связанные с полиномами.
Радикал, обращающий функцию в ноль
Рассмотрим ситуацию, когда при подстановке значения х в радикал, результат равен нулю. В таких случаях, можем говорить о корнях уравнения. Характеристика корней позволяет нам определить количество и тип (действительные, комплексные, кратные) решений, что приносит ценность в решении математических задач и анализе функций.
Поиск соответствующих значений х производится с помощью алгебраических методов решения уравнений. Для каждой функции с радикалом прописывается математическое выражение, исходя из которого находим значения х при нулевой функции.
Знание значений х, при которых радикал равен нулю, помогает нам анализировать и интерпретировать данные задачи и обнаруживать возможные особенности и граничные случаи.
Когда логарифм обращается в ноль

Такой коэффициент x может быть интерпретирован как точка на графике функции, где она пересекает ось абсцисс, обозначая переход от положительной величины к отрицательной или наоборот. Это также может быть полезно для окончательного определения областей допустимых значений, где логарифмическая функция несуществуют или являются бесконечными.
Вопрос-ответ

Что такое преобразованная функция?
Преобразованная функция - это функция полученная путем применения определенного преобразования к исходной функции. В данной статье мы рассматриваем значения х, при которых значение преобразованной функции равно нулю.
Как найти значение х, при котором значение преобразованной функции равно нулю?
Для того чтобы найти значение х, при котором значение преобразованной функции равно нулю, необходимо решить уравнение, полученное из преобразования функции. Решив это уравнение, мы найдем искомое значение х.
Можно ли привести пример преобразованной функции, значение которой равно нулю при определенном х?
Да, конечно! Например, рассмотрим функцию f(x) = x^2 - 4. Преобразуем ее, добавив 2 к х вместо x. Получим функцию f(x-2) = (x-2)^2 - 4. Значение этой функции будет равно нулю при х = 4.
Какие методы можно использовать для нахождения значения х, при котором значение преобразованной функции равно нулю?
Для решения уравнений, из которых получены преобразованные функции, можно использовать различные методы, такие как метод подстановки, метод графического интерпретирования, метод параболы и другие. Выбор метода зависит от конкретной функции и условий задачи.
Можно ли найти несколько значений х, при которых значение преобразованной функции равно нулю?
Да, вполне возможно найти несколько значений х, при которых значение преобразованной функции равно нулю. Количество таких значений может быть различным и зависит от формы исходной функции, а также от применяемого преобразования.
Как найти значение х, при котором значение преобразованной функции равно нулю?
Чтобы найти значение х, при котором значение преобразованной функции равно нулю, нужно решить уравнение, полученное из данной функции приравниванием ее значения к нулю. Решив уравнение, вы найдете значение х, которое удовлетворяет заданному условию.