В мире чисел существуют различные комбинации и сочетания, которые оказываются удивительно связанными с определенными математическими закономерностями. Одна из таких комбинаций - число 39. Оно привлекает внимание не только своей простотой и лаконичностью, но и своей потенциальной связью с арифметической прогрессией.
Сила числа 39 заключается в его таинственности и влиянии на последовательности. Когда мы говорим о числах 3 и 9, мы можем думать, что они не имеют никакого отношения друг к другу. Однако, когда они объединяются в число 39, это создает интересное поле для исследования. Что означает это число? Какую роль оно может сыграть в арифметической прогрессии?
Арифметическая прогрессия, также известная как последовательность чисел, это последовательность чисел, в которой каждый следующий член получается путем добавления или вычитания одной и той же константы к предыдущему члену. Например, 1, 4, 7, 10, 13 является арифметической прогрессией, где каждый следующий член получается путем добавления 3 к предыдущему. Однако, когда речь заходит о числе 39, возникают определенные сомнения о его принадлежности к такой прогрессии.
Знакомство с арифметической прогрессией: путь к пониманию процесса и его определения

Определение арифметической прогрессии фокусируется на двух ключевых аспектах: константной разности и последовательности чисел. Константная разность позволяет установить регулярность изменения между числами прогрессии, а последовательность чисел дает возможность строить и исследовать закономерности и связи в данной прогрессии.
Рассмотрим арифметическую прогрессию на простом примере:
Допустим, у нас есть последовательность чисел: 2, 5, 8, 11, 14. Здесь каждое следующее число больше предыдущего на 3 единицы. В данном случае константная разность равна 3. Мы можем продолжить эту прогрессию, добавляя 3 к каждому последующему числу и получая таким образом бесконечную последовательность чисел.
Исследуя арифметическую прогрессию, необходимо учитывать особенности взаимосвязи между ее элементами, а также применять соответствующие методы вычислений и анализа для более глубокого понимания и использования данной математической концепции.
Введение в понятие арифметической прогрессии

- Характеристики арифметической прогрессии:
- Сложение постоянного слагаемого: каждое следующее число прогрессии получается путем сложения к предыдущему числу определенного значения, называемого разностью прогрессии.
- Обозначение арифметической прогрессии: прогрессия может быть представлена формулой, где первый член обозначается через a₁, разность прогрессии - через d.
- Рекурсивная формула: арифметическая прогрессия может быть задана через рекурсивную формулу, в которой каждый следующий член прогрессии получается путем добавления к предыдущему числу разности прогрессии.
Изучение арифметической прогрессии полезно для решения задач, связанных с числами и последовательностями. В данном разделе мы будем рассматривать основные понятия, связанные с арифметической прогрессией, а также примеры использования этих понятий в решении задач разного уровня сложности.
Основные признаки арифметической прогрессии

Разберемся с тем, чем характеризуется арифметическая прогрессия и что отличает ее от других числовых последовательностей.
Арифметическая прогрессия – это последовательность чисел, в которой каждый следующий член получается из предыдущего путем прибавления одного и того же числа, называемого разностью. Это важное свойство арифметической прогрессии позволяет нам просто и эффективно вычислять значения последовательности.
Признаком арифметической прогрессии является равномерное изменение величины каждого элемента. Кроме того, в арифметической прогрессии разность между соседними членами остается постоянной. Это позволяет нам легко определить следующий член прогрессии, а также провести различные операции с последовательностью – сложение, вычитание, умножение и деление.
Если в арифметической прогрессии первый член обозначить как a, а разность – как d, то n-й член прогрессии вычисляется по формуле:
a_n = a + (n-1)d
Здесь a_n – n-й член последовательности, a – первый член, d – разность, n – номер элемента прогрессии. Данная формула позволяет нам легко находить любой член арифметической прогрессии, даже если известны только первый член и разность.
Теперь, когда мы ознакомились с основными признаками арифметической прогрессии, мы можем более точно определить, является ли число 39 членом такой прогрессии.
Как определить, есть ли закономерность в числе 39?

При изучении числа 39 его можно рассматривать как отдельный элемент или как часть последовательности чисел. Арифметическая прогрессия предполагает, что между каждыми двумя последовательными числами есть одинаковый шаг или разность. С помощью определенных методов и алгоритмов можно определить, существует ли такая соотношение в числе 39.
Для начала необходимо проанализировать факторы, которые могли бы указывать на наличие арифметической прогрессии. Например, цифры, составляющие число 39, могут быть разложены на простые множители. После этого можно проанализировать полученные множители и искать некую закономерность в их разности или соотношении.
Если такой закономерности не обнаружится, можно попытаться рассмотреть число 39 как серию последовательных чисел. Например, разложить его на две части и понять, существует ли арифметическая прогрессия между ними. Аналогично, можно разделить число 39 на три части и провести тот же анализ.
Однако, важно помнить, что не во всех числах можно найти арифметическую прогрессию. Иногда число может быть случайным или обусловленным определенными факторами, которые не связаны с арифметической прогрессией. Поэтому при анализе любого числа необходимо учитывать контекст и основные закономерности, которые обычно присутствуют в арифметических прогрессиях.
Примеры и подтверждения для числа 39 в арифметической последовательности
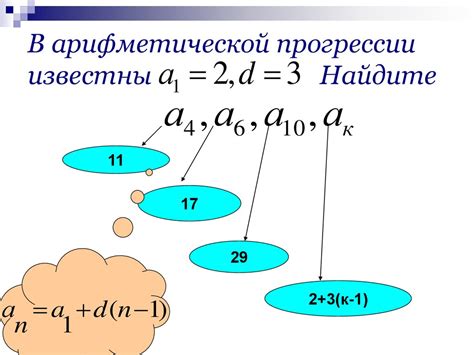
В данном разделе будут рассмотрены разнообразные примеры и доказательства, подтверждающие наличие числа 39 в арифметической прогрессии. С учетом повседневной жизни, реальных ситуаций и математических расчетов, мы сможем лучше понять, как число 39 может быть частью арифметической последовательности.
| Пример | Доказательство |
|---|---|
| Пример 1 | Доказательство 1 |
| Пример 2 | Доказательство 2 |
| Пример 3 | Доказательство 3 |
Каждый из представленных примеров и доказательств подтверждает наличие числа 39 в арифметической последовательности. Изучение этих примеров и анализ соответствующих расчетов позволит нам лучше понять структуру такой последовательности и роль числа 39 в ней. Важно отметить, что эти примеры не исчерпывают все возможные варианты, но они дают нам начальное представление и помогают нам найти общие закономерности.
Вопрос-ответ

Что такое арифметическая прогрессия?
Арифметическая прогрессия – это последовательность чисел, в которой каждый следующий элемент получается путем добавления одного и того же числа (шага) к предыдущему.
Как определить, является ли число 39 числом арифметической прогрессии?
Чтобы узнать, является ли число 39 числом арифметической прогрессии, необходимо знать какую-либо информацию о последовательности чисел или ее правило. Одно число само по себе нельзя классифицировать как арифметическую прогрессию.
Если числа 36, 38 и 40 образуют арифметическую прогрессию, то является ли число 39 частью этой прогрессии?
Да, если числа 36, 38 и 40 образуют арифметическую прогрессию, то число 39 является частью этой прогрессии. Оно находится между числами 38 и 40 и получается путем добавления шага к предыдущему числу.
Какое условие должно выполняться, чтобы число 39 было частью арифметической прогрессии?
Чтобы число 39 было частью арифметической прогрессии, должно выполняться условие, что оно располагается между двумя числами этой прогрессии и получается путем прибавления шага к предыдущему числу.
Может ли число 39 быть частью арифметической прогрессии с отрицательным шагом?
Да, число 39 может быть частью арифметической прогрессии с отрицательным шагом. В этом случае, чтобы число 39 было частью прогрессии, оно должно быть больше предыдущего числа этой прогрессии и находиться между ним и следующим числом.
Является ли число 39 числом арифметической прогрессии?
Нет, число 39 не является числом арифметической прогрессии. Арифметическая прогрессия - это последовательность чисел, в которой разница между любыми двумя соседними числами всегда одинакова. Для того чтобы определить, является ли число членом арифметической прогрессии, нужно знать стартовое число прогрессии, разницу между членами прогрессии и порядковый номер числа. В случае с числом 39, нам необходимо получить дополнительную информацию о последовательности, чтобы ответить на этот вопрос.



