Когда мы говорим о геометрии и векторных величинах, необходимо осознать, что каждый объект этой науки имеет свою уникальную символику и специфическое значение. И одним из самых важных и распространенных символов являются две стрелки, направленные вверх. Объекты, обозначаемые этими стрелками, представляют собой действительные или абстрактные направленные величины, и их роль в геометрии невозможно переоценить.
Когда мы впервые обращаем внимание на эти две стрелки, можем не задумываться о том, что они имеют глубокое философское значение и сочетают прошлое, настоящее и будущее. Ведь их использование связано не только с математическими расчетами и анализом геометрических объектов, но и с идеей движения, развития, преодоления преград и достижения целей.
Две стрелки, указывающие вверх, являются не только символическим обозначением векторов в геометрии, но и отражают естественные явления, которые окружают нас в повседневной жизни. Эти стрелки символизируют не только направление в пространстве, но и наше стремление к постоянному развитию и прогрессу. Они представляют собой нечто большее, чем просто элементы математического языка, они символизируют наше присутствие в мире и наше непрерывное движение вперед.
Основные концепции и идеи в геометрии векторов: символическое обозначение с двумя стрелочками вверх
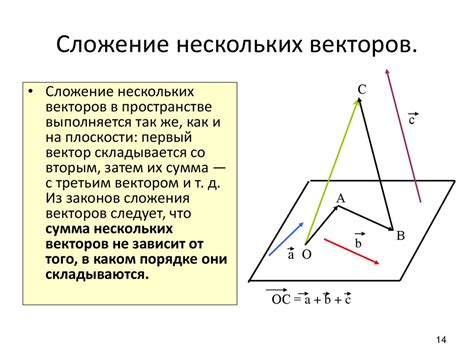
Использование символа с двумя стрелочками вверх позволяет наглядно обозначить направление вектора в пространстве. Это визуальное представление помогает установить ориентацию вектора и понять его направление относительно других объектов в системе координат.
| Аспект | Описание |
|---|---|
| Направление | Символ с двумя стрелочками вверх указывает направление вектора от начала координат к его конечной точке. |
| Масштабирование | Символическое обозначение с двумя стрелочками вверх позволяет определить длину вектора, хотя сам символ не имеет единиц измерения. |
| Визуальное представление | Использование этого символа помогает создать графическое изображение векторов и упростить представление о взаимодействии векторных величин в конкретной задаче. |
Векторное пространство: основные понятия и свойства

Векторы, в отличие от чисел, могут быть представлены геометрическими объектами, такими как направленные отрезки на плоскости или в пространстве. Они подчиняются некоторым законам и операциям, с помощью которых мы можем выполнять различные арифметические действия.
Векторное пространство определяется набором векторов и набором операций между ними. Операции включают сложение векторов и умножение вектора на число, которые обладают определенными свойствами, такими как коммутативность, ассоциативность и дистрибутивность. Кроме того, в векторном пространстве существует нулевой вектор, обозначающийся обычно символом 0, и векторы, обратные друг другу.
Важно отметить, что векторное пространство может иметь различные размерности - от одномерного до бесконечномерного. Каждая размерность имеет свои особенности и применения в различных областях науки, таких как физика, информатика, экономика и др.
Понимание основных понятий и свойств векторного пространства является важным фундаментом для изучения более сложных концепций, таких как линейная зависимость и независимость, базисы и линейные преобразования. Эти понятия играют ключевую роль в решении различных задач, включая анализ данных, моделирование и оптимизацию.
Линейная зависимость векторов и равенство нулевого вектора

Обсудим существенные аспекты линейной зависимости векторов и связанное с ней равенство нулевого вектора. Векторы, как направленные отрезки, могут быть линейно зависимыми, что означает, что один вектор может быть выражен через другие с помощью линейных комбинаций, состоящих из коэффициентов и соответствующих векторов. Однако, если векторы линейно зависимы, это значит, что они имеют нулевую линейную комбинацию, где все коэффициенты равны нулю. В таком случае, эти векторы становятся равными нулевому вектору, который не имеет определенного направления и длины.
Векторное сложение и вычитание: геометрическая интерпретация

Сложение векторов можно представить в виде перемещения точки из начального положения в конечное положение. Геометрический смысл сложения заключается в том, что мы объединяем два вектора таким образом, чтобы конец одного вектора совмещался с началом другого вектора. В результате получается новый вектор, который имеет начало в начале первого вектора и конец в конце второго вектора. Таким образом, сумма векторов позволяет получить итоговое перемещение точки.
Вычитание векторов, в свою очередь, можно представить в виде перемещения точки из начального положения в конечное положение, но с обратным направлением. Геометрически это означает, что мы откладываем второй вектор от конца первого вектора, получая новый вектор, который начинается в начале первого вектора и заканчивается в конце второго вектора. Вычитание векторов позволяет нам определить перемещение точки в обратном направлении.
- При векторном сложении важными свойствами являются ассоциативность и коммутативность. Ассоциативность означает, что порядок, в котором выполняется сложение не важен, и результат остаётся неизменным. Коммутативность же говорит о том, что результат сложения двух векторов не зависит от их порядка.
- Результатом векторного вычитания является вектор, полученный при сложении исходного вектора со вторым вектором, у которого изменено направление.
- Векторное сложение и вычитание активно применяются в различных областях науки и техники, таких как физика, механика, компьютерная графика и др.
Итак, геометрическая интерпретация векторного сложения и вычитания позволяет наглядно представить перемещение точки при суммировании и отнимании векторов. Сложение векторов осуществляется путем объединения их начал и концов, а вычитание - путем откладывания одного вектора от конца другого. Эти операции обладают важными свойствами и широко применяются в различных областях науки и техники.
Умножение вектора на число: изменение длины и направления

При умножении вектора на положительное число, мы расширяем вектор, увеличивая его длину в соответствии с заданным множителем. В то же время, направление вектора остается неизменным. Это позволяет нам контролировать масштаб вектора и его протяженность в пространстве.
В случае умножения вектора на отрицательное число, мы не только изменяем длину вектора, но и меняем его направление. Вектор приобретает противоположный характер и указывает в обратную сторону от начальной точки. Таким образом, через операцию умножения на отрицательное число мы можем осуществлять отражение вектора относительно начала координат.
Умножение вектора на число находит свое применение в различных сферах, включая физику, экономику, компьютерную графику и другие. Например, в физике это позволяет определить силу, действующую на объект в определенном направлении и с определенной величиной. В компьютерной графике умножение вектора на число используется для масштабирования объектов и создания анимации.
Физическая интерпретация верхних стрелок в геометрии векторов
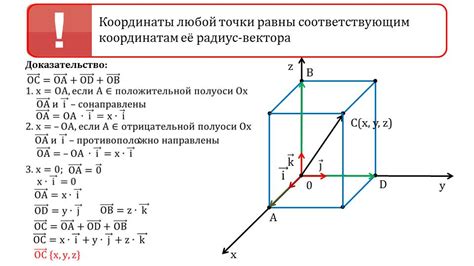
В физике, где векторы играют важную роль, использование верхних стрелок существенно расширяет возможности геометрической интерпретации. Векторы с верхними стрелками подразумевают направление движения или векторную величину в пространстве, в отличие от безразмерных скоростей или модулей векторов.
Векторные величины с верхними стрелками могут описывать различные физические параметры, такие как скорость, ускорение, сила или импульс. Направление и величина вектора задаются координатами или компонентами, которые могут быть представлены как символы или числа с верхними стрелками.
Конкретные физические примеры включают в себя векторы скорости, которые описывают движение тела в определенном направлении и соответствующей скорости. Вектор ускорения указывает на изменение скорости со временем и позволяет описать изменение траектории движения. Сила, которая представляет собой векторную величину, может быть понята как причина изменения скорости или направления движения объекта.
Использование верхних стрелок в физических применениях геометрии векторов позволяет наглядно и ясно представить векторные величины и их взаимодействие. Такая интерпретация помогает упростить моделирование физических процессов и облегчает понимание исследуемых явлений. Векторы с верхними стрелками являются мощным инструментом в физике и смежных областях науки.
Интерпретация двух стрелок вверх как направления и силы
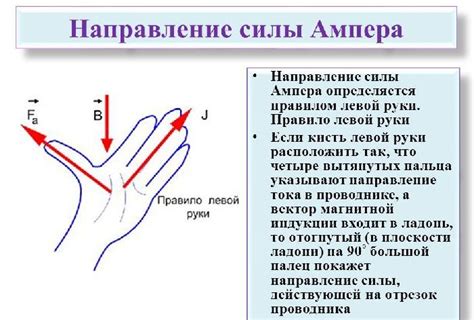
Рассмотрим интерпретацию символа, состоящего из двух стрелок, направленных вверх, в контексте геометрии векторов. Этот символ может быть понят как указание на конкретное направление и силу действия.
Один из аспектов интерпретации этого символа - подчеркнуть направление, в котором вектор указывает. Подобно стрелкам на компасе, две стрелки вверх могут служить ориентиром для понимания, в каком направлении действует вектор. Они помогают нам представить, что вектор движется вверх по отношению к другим объектам или системе координат.
Второй аспект интерпретации символа связан с его силой. Две стрелки вверх могут символизировать не только направление движения вектора, но и его силу или интенсивность. Чем длиннее стрелки вверх, тем больше сила действия вектора.
Применение данной интерпретации символа может быть обосновано в различных сферах, где имеется потребность в ясном указании направления и силы векторного действия. Например, это может быть полезно в физике или инженерных расчётах, где необходимо четко представить, как вектор воздействует на объект или конструкцию. Также данный символ может иметь значение в области географии или навигации, помогая ориентироваться в пространстве и следовать заданным маршрутам.
Анализ двух стрелок вверх в физических задачах: примеры
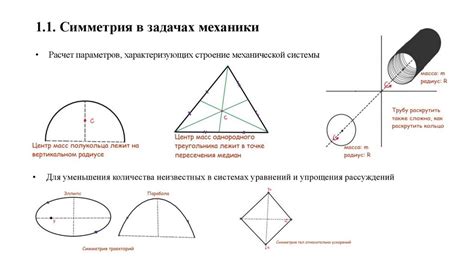
Этот раздел посвящен анализу и примерам использования концепции двух стрелок вверх в физических задачах. Используя соответствующие понятия и методы, будем изучать особенности и значимость этого явления.
Представим ситуацию, где две стрелки направлены вверх. Их взаимное расположение и векторные характеристики могут указывать на определенные физические процессы или закономерности.
Один из примеров употребления двух стрелок вверх - при изучении движения тел в гравитационном поле Земли. В этом случае, направление стрелок и их относительные величины могут указывать на силу тяжести и противодействующие силы, такие как сопротивление воздуха или поддерживающая сила.
Другой пример - векторное сложение сил. Если две стрелки вверх представляют силы, то их взаимное расположение и направления могут помочь определить итоговую силу, действующую в системе.
Практическое использование конструкции с двумя стрелочками вверх в векторной геометрии

Ориентация:
Расположение двух стрелочек вверх в векторной геометрии указывает на направление вектора в пространстве. Эта ориентация позволяет точно определить, какой конец вектора считается началом, а какой – концом. Таким образом, две стрелочки вверх выступают в роли визуального индикатора, обозначая, где начало, а где конец вектора.
Отношение величин:
Векторы в геометрии могут иметь различную длину и направление. Конструкция с двумя стрелочками вверх используется для отображения отношения величин векторов. Если два вектора одинаковы по направлению и длине, то они могут быть представлены с одной и той же конструкцией с двумя стрелочками вверх.
Графическое представление:
Векторы часто представляются в виде стрелок на графиках и диаграммах. При использовании конструкции с двумя стрелочками вверх, можно наглядно представить направление и масштаб вектора. Такое графическое представление позволяет легче воспринимать информацию о векторах и использовать их в различных практических задачах, таких как физические расчеты, моделирование движения и многие другие.
Применение векторов в разнообразных областях науки и техники

Векторы, являющиеся измеримыми величинами, играют важную роль в многих различных областях науки и техники. Они часто применяются для описания и анализа физических явлений и процессов, а также в различных прикладных задачах. Векторное представление позволяет учитывать не только величину, но и направление физической величины, что делает его незаменимым инструментом для решения разнообразных задач.
| Область | Примеры применения |
|---|---|
| Механика | Анализ движения тел, расчет силы трения, определение равновесия системы |
| Электродинамика | Расчет силы магнитного поля на заряженные частицы, моделирование электромагнитных волн |
| Теплопередача | Описания тепловых потоков, расчеты тепловых потерь в системах |
| Гидродинамика | Исследование потоков жидкости и газа, моделирование аэродинамических процессов |
| Оптика | Определение направления распространения света, моделирование лучей света |
| Биология | Изучение движения организмов, моделирование сил, действующих на клетки |
Векторы также находят широкое применение в технике, например, в архитектуре и конструкционном проектировании для анализа сил в строительных элементах, в авиации и космонавтике для моделирования полетов и расчета траекторий, а также в информационных технологиях для работы с графическими изображениями и обработки сигналов. С использованием векторов возможно более точное и эффективное решение сложных задач, что делает их неотъемлемой частью многих научных и технических дисциплин.
Решение задач с использованием двух стрелочек вверх: алгоритмы и методы

Рассмотрение данной темы открывает перед нами огромные возможности для углубленного изучения специфики и функциональных особенностей этих двух символов в контексте геометрии векторов. Мы обратимся к обсуждению алгоритмов и методов, позволяющих успешно применять эти символы для решения разнообразных задач.
Алгоритмы и методы, основанные на использовании двух стрелочек вверх, открывают широкий спектр возможностей для анализа, моделирования, прогнозирования и оптимизации геометрических процессов.
Определение геометрических параметров, вычисление направления и масштабирование векторов, нахождение оптимальных путей и расстояний, исследование областей пространства – все эти задачи становятся доступными и эффективными благодаря использованию двух символов стрелочек, направленных вверх.
Алгоритмы и методы, базирующиеся на этих символах, предлагаются в виде последовательности логически связанных шагов, позволяющих систематически разбираться с задачами и достигать желаемых результатов с минимальными усилиями.
Основная цель данного раздела – представить основные аспекты, которые следует учесть при использовании двух символов стрелочек вверх при решении геометрических задач, а также научить читателя применять различные алгоритмы и методы.
Стремление к освоению этих алгоритмов и методов позволит не только с легкостью справляться с задачами геометрии векторов, но и находить новые подходы к решению других сложных математических проблем.
Вопрос-ответ

Зачем нужны две стрелочки вверх в геометрии векторы?
Две стрелочки вверх в геометрии векторы используются для отображения направления вектора. Одна стрелочка указывает на начало вектора, а другая на его конец. Таким образом, две стрелочки позволяют наглядно представить, в каком направлении расположен вектор.
Можно ли использовать одну стрелочку вместо двух в геометрии векторы?
В геометрии векторы обычно обозначаются двумя стрелками вверх, чтобы указать на их направление. Однако, можно использовать одну стрелку, но в этом случае будет сложнее определить направление вектора. Поэтому, в основном, используются две стрелки вверх для лучшей наглядности и удобства визуализации векторов.